機械学習の技術は、ビジネスや意思決定プロセスにおいてますます重要性を増しています。
しかし、意思決定者にとって重要なのは、機械学習モデルがどのくらい精度が高いのかとかSOTAなのかとかではなく、実際の意味で役立つかという点です。
それはビジネスオペレーション運用の観点での実現可能性であったり、利益やコストのインパクト目線で意味があるのかといった点です。
本記事では、表題の通り、クレジットカードの不正利用を予測するモデルの実装を題材として、損益行列を用いてインパクトの目線で機械学習モデルを評価する流れに焦点を当ててみたいと思います。
こういったビジネス目線において意味のある機械学習などのデータサイエンスに関するノウハウとして以下の書籍が参考になります。
データの確認と準備
Kaggleデータセットにクレジットカードの利用履歴データを主成分化したいくつかのカラムと、それが不正利用であったかどうかラベル付けされているデータがあります。
今回はこのデータを用いて、クレジットカードの不正利用予測モデルを作ってみて評価するところまでを行います。
元々特徴量はほとんどが主成分化されているため、どのカラムがどういった内容を表すのかは不明です。
また、欠損値もありません。
クラスについて集計をしてみますと以下のようにかなり不均衡なデータになっています。
この辺りはリアルでも不正利用というデータは稀だと思いますので、よくある設定だと思います。
| データ件数 | 不正利用フラグ=1の件数 | 不正利用データの割合 |
|---|---|---|
| 284,807件 | 492件 | 0.00173 |
相関行列のヒートマップを可視化してみると以下のような感じです。
(不正利用クラスのカラムは最下行/最右列のClassの項目)
特別どこかのカラムにすごく相関しているとかではなさそうです。
df = pd.read_csv('./data/creditcard.csv')
plt.figure(figsize=(18,15))
sns.heatmap(df.corr(), annot=True, vmax=1, vmin=-1, fmt='.1f', cmap=cm)
plt.show()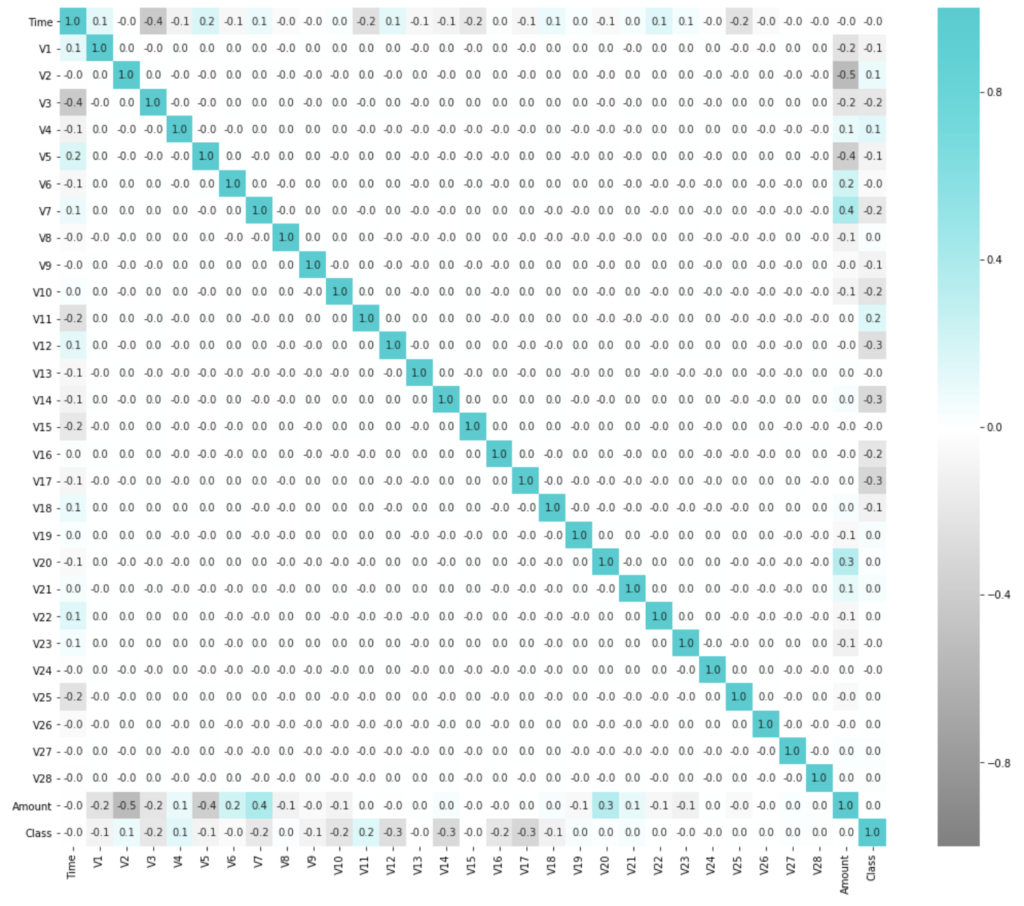
教師データを作成していこうと思います。
上記の通り、クラス別のサンプル数がかなり偏っていますので、ちゃんとモデルを学習させられるようにデータをサンプリングして偏りを揃えます。
アンダーサンプリングやオーバーサンプリングなどが揃っているライブラリimblearnを使います。
from imblearn import under_sampling, over_sampling
cols = df.columns.tolist()
cols.remove('Class')
positive_cnt = int(df['Class'].sum())
rus = under_sampling.RandomUnderSampler(sampling_strategy={0:positive_cnt, 1:positive_cnt}, random_state=0)
data_x_sample, data_y_sample = rus.fit_sample(df[cols], df[['Class']])
len(data_x_sample), len(data_y_sample), df['Class'].sum()(984, 984, 492)
不正取引Class = 1が圧倒的に少ないので、これに合わせるように不正取引でないデータをアンダーサンプリングしました。
次に使う特徴量をいくつかにピックアップしようと思います。
分類モデルの学習に効く特徴量を探すため、scikit-learnに実装されているRFECVを使います。
再帰的特徴除去(Recursive Feature Elimination: RFE)は、変数減少法と同じく、最初に全ての特徴量を使ってモデルを学習し、最も重要度の低いを特徴量を除去して、性能を再計算するという処理を繰り返していきます。
重要度の指標にはfeature_importancesやcoefが使われます。
これを交差検証の中で行うのがRFECVです。
# 特徴量を選択する
feature_importance_models = [
ensemble.AdaBoostClassifier(),
ensemble.ExtraTreesClassifier(),
ensemble.GradientBoostingClassifier(),
ensemble.RandomForestClassifier(),
tree.DecisionTreeClassifier(),
XGBClassifier()
]
scoring = ['accuracy']
df_rfe_cols_cnt = pd.DataFrame(columns=['cnt'], index=cols)
df_rfe_cols_cnt['cnt'] = 0
for i, model in tqdm(enumerate(feature_importance_models), total=len(feature_importance_models)):
rfe = feature_selection.RFECV(model, step=3)
rfe.fit(data_x_sample, data_y_sample)
rfe_cols = df[cols].columns.values[rfe.get_support()]
df_rfe_cols_cnt.loc[rfe_cols, 'cnt'] += 1
df_rfe_cols_cnt.plot(kind='bar', color=base_color, figsize=(15, 5))
plt.show()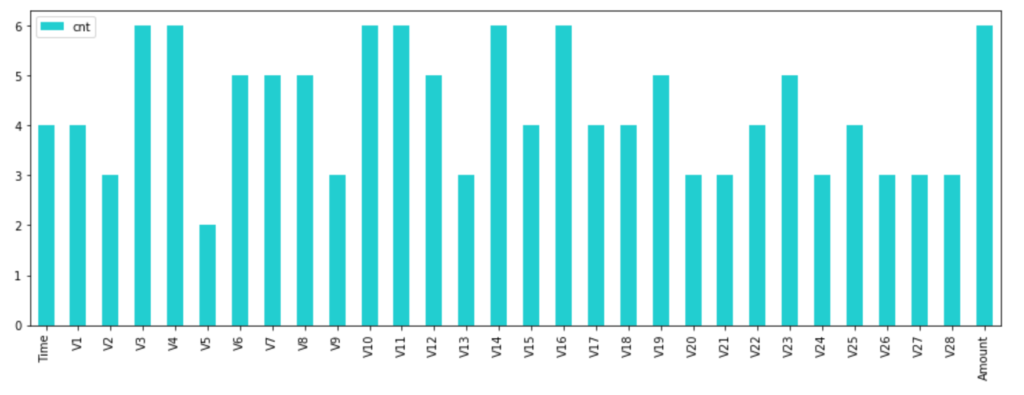
このような形で、どの変数がどのくらい選ばれたかが分かります。
上記6つのモデル中4つ以上のモデルから選択された、以下の特徴量らを使うことにしました。
x_cols = df_rfe_cols_cnt[df_rfe_cols_cnt['cnt'] >= 4].index
x_colsIndex(['Time', 'V1', 'V3', 'V4', 'V6', 'V7', 'V8', 'V10', 'V11', 'V12', 'V14',
'V15', 'V16', 'V17', 'V18', 'V19', 'V22', 'V23', 'V25', 'Amount'],
dtype='object')モデル学習
それではモデルを作ってみます。
今回はデータ自体は主成分化されて簡単な状態ですので、いくつかの代表的なモデルを使った投票モデルを作ってみようと思います。
まずはじめに複数のモデルを学習させてみます。
後で精度を見ながらモデルを選びますので、ひとまず思いついたものを適当にぶち込んでみました。
# 特徴量を選択して複数のモデルで精度を調査する
models = [
#Ensemble Methods
ensemble.AdaBoostClassifier(),
ensemble.BaggingClassifier(),
ensemble.ExtraTreesClassifier(),
ensemble.GradientBoostingClassifier(),
ensemble.RandomForestClassifier(),
#Gaussian Processes
gaussian_process.GaussianProcessClassifier(),
#GLM
linear_model.LogisticRegressionCV(),
linear_model.RidgeClassifierCV(),
#Navies Bayes
naive_bayes.BernoulliNB(),
naive_bayes.GaussianNB(),
#Nearest Neighbor
neighbors.KNeighborsClassifier(),
#Trees
tree.DecisionTreeClassifier(),
tree.ExtraTreeClassifier(),
#Discriminant Analysis
discriminant_analysis.LinearDiscriminantAnalysis(),
discriminant_analysis.QuadraticDiscriminantAnalysis(),
#xgboost
XGBClassifier()
]
df_compare = pd.DataFrame(columns=['name', 'train_accuracy', 'valid_accuracy', 'time'])
scoring = ['accuracy']
# 学習と精度評価
for model in tqdm(models):
name = model.__class__.__name__
cv_rlts = model_selection.cross_validate(model, data_x_sample, data_y_sample, scoring=scoring, cv=10, return_train_score=True)
for i in range(10):
s = pd.Series([name, cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name=name+str(i))
df_compare = df_compare.append(s)
plt.figure(figsize=(12,8))
sns.boxplot(data=df_compare, y='name', x='valid_accuracy', orient='h', color=base_color, linewidth=0.5, width=0.5)
plt.grid()
plt.show()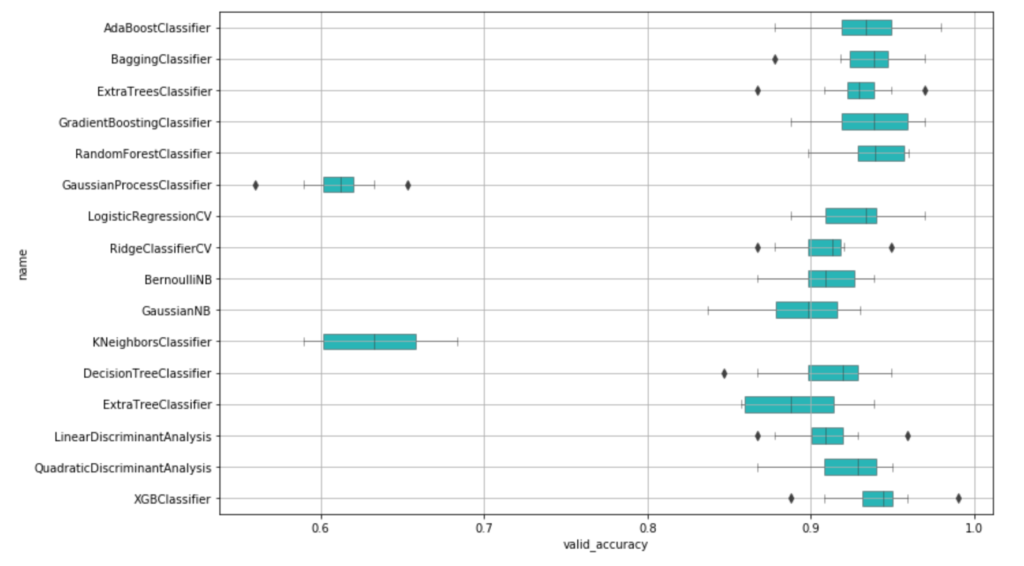
XGBoostに続いて、AdaBoost、バギング、勾配Boosting辺りが良さそうです。valid_accuracyで平均して確認してみると以下のような感じです。
df_compare.groupby('name').mean().sort_values(by='valid_accuracy', ascending=False)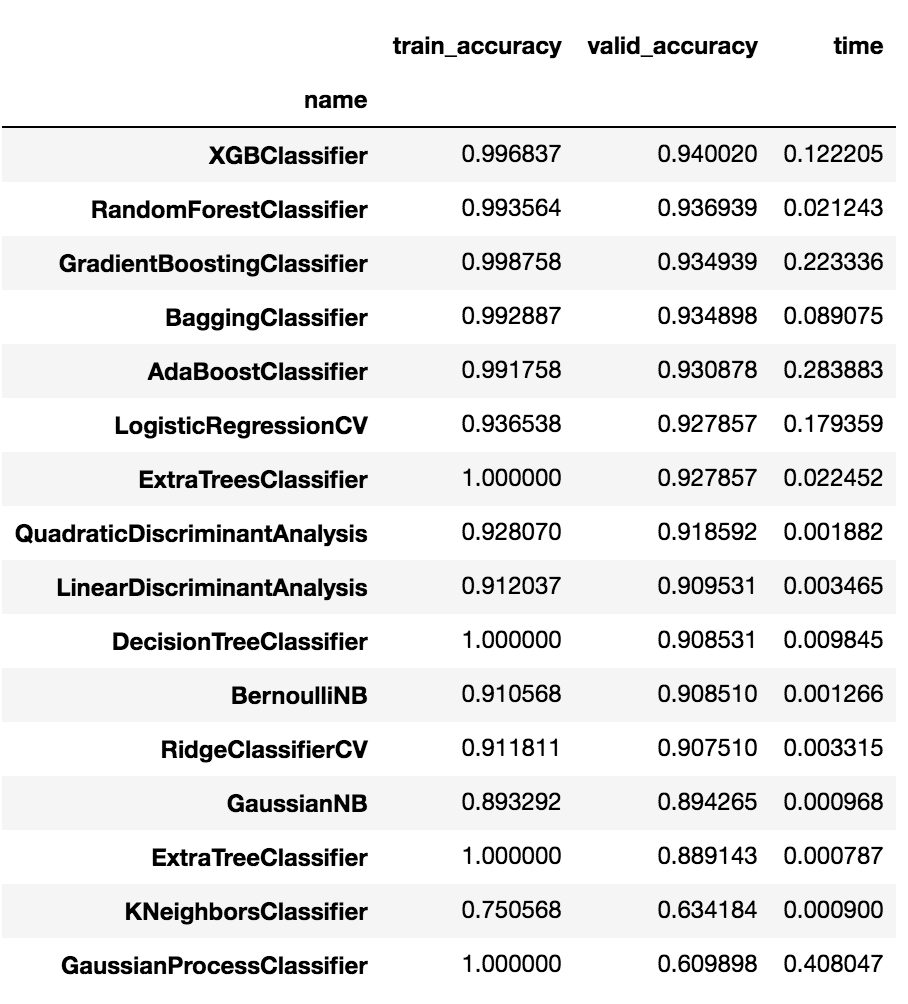
最高で94.0%の精度と、非常に良い精度が出ています。
続いて、93.6%、93.4%、…と続いています。
それではさらにこの中から精度の良いモデルを複数選んで、まずはハイパーパラメータをデフォルトのままで投票モデルを学習させてみます。
# 精度の良いモデルを選んで、投票モデルを学習
vote_models = [
#Ensemble Methods
('abc', ensemble.AdaBoostClassifier()),
('bc', ensemble.BaggingClassifier()),
('etsc', ensemble.ExtraTreesClassifier()),
('gbc', ensemble.GradientBoostingClassifier()),
('rfc', ensemble.RandomForestClassifier()),
#Gaussian Processes
#('gpc', gaussian_process.GaussianProcessClassifier()),
#GLM
('lrcv', linear_model.LogisticRegressionCV()),
#('rccv', linear_model.RidgeClassifierCV()), # unable soft voting
#Navies Bayes
#('bnb', naive_bayes.BernoulliNB()),
#('gnb', naive_bayes.GaussianNB()),
#Nearest Neighbor
#('knc', neighbors.KNeighborsClassifier()),
#Trees
#('dtc', tree.DecisionTreeClassifier()),
#('etc', tree.ExtraTreeClassifier()),
#Discriminant Analysis
#('lda', discriminant_analysis.LinearDiscriminantAnalysis()),
#('qda', discriminant_analysis.QuadraticDiscriminantAnalysis()),
#xgboost
('xgbc', XGBClassifier())
]
df_compare = pd.DataFrame(columns=['name', 'train_accuracy', 'valid_accuracy', 'time'])
scoring = ['accuracy']
# Hard Voteモデル
vote_hard_model = ensemble.VotingClassifier(estimators=vote_models, voting='hard')
cv_rlts = model_selection.cross_validate(vote_hard_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
s = pd.Series(['hard', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='hard'+str(i))
df_compare = df_compare.append(s)
# Soft Voteモデル
vote_soft_model = ensemble.VotingClassifier(estimators=vote_models , voting='soft')
cv_rlts = model_selection.cross_validate(vote_soft_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
s = pd.Series(['soft', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='soft'+str(i))
df_compare = df_compare.append(s)
plt.figure(figsize=(12,3))
sns.boxplot(data=df_compare, y='name', x='valid_accuracy', orient='h', color=base_color, linewidth=0.5, width=0.5)
plt.grid()
plt.show()
df_compare.groupby('name').mean().sort_values(by='valid_accuracy', ascending=False)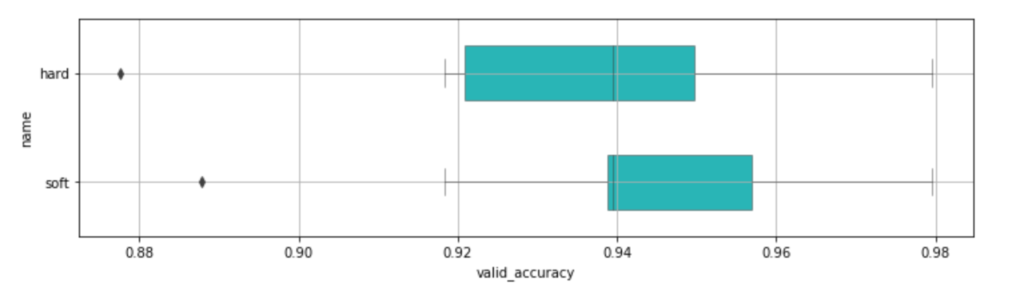
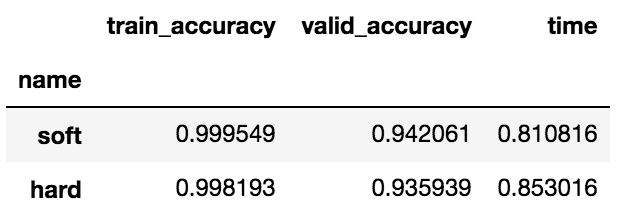
投票モデルを使うことで、精度が94.2%に上がりました。
後にスコアリングしたいのでpredict_probaが使えるsoftしか使いませんが、念のためhardも出しておきました。hardは単純に利用した各モデルの予測を多数決してクラスを予測します。
一方softは利用した各モデルのそれぞれのpredict_probaによる予測確率の平均値をとって最終的にクラスを予測します。
さて、さらにグリッドサーチを行って、各モデルで最適なハイパーパラメータを選択して、再度投票モデルを学習させてみます。
# 各モデルのハイパーパラメータをグリッドサーチ
grid_n_estimator = [10, 50, 100, 300]
grid_ratio = [.1, .25, .5, .75, 1.0]
grid_learn = [.01, .03, .05, .1, .25]
grid_max_depth = [2, 4, 6, 8, 10, None]
grid_min_samples = [5, 10, .03, .05, .10]
grid_criterion = ['gini', 'entropy']
grid_bool = [True, False]
grid_seed = [0]
grid_param = [
#AdaBoostClassifier
[{
'n_estimators': grid_n_estimator, #default=50
'learning_rate': grid_learn, #default=1
#'algorithm': ['SAMME', 'SAMME.R'], #default=’SAMME.R
'random_state': grid_seed
}],
#BaggingClassifier
[{
'n_estimators': grid_n_estimator, #default=10
'max_samples': grid_ratio, #default=1.0
'random_state': grid_seed
}],
#ExtraTreesClassifier
[{
'n_estimators': grid_n_estimator, #default=10
'criterion': grid_criterion, #default=”gini”
'max_depth': grid_max_depth, #default=None
'random_state': grid_seed
}],
#GradientBoostingClassifier
[{
#'loss': ['deviance', 'exponential'], #default=’deviance’
'learning_rate': [.05], #default=0.1
'n_estimators': [300], #default=100
#'criterion': ['friedman_mse', 'mse', 'mae'], #default=”friedman_mse”
'max_depth': grid_max_depth, #default=3
'random_state': grid_seed
}],
#RandomForestClassifier
[{
'n_estimators': grid_n_estimator, #default=10
'criterion': grid_criterion, #default=”gini”
'max_depth': grid_max_depth, #default=None
'oob_score': [True], #default=False
'random_state': grid_seed
}],
#LogisticRegressionCV
[{
'fit_intercept': grid_bool, #default: True
#'penalty': ['l1','l2'],
'solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'], #default: lbfgs
'random_state': grid_seed
}],
# ExtraTreeClassifier
[{}],
# LinearDiscriminantAnalysis
[{}],
#XGBClassifier
[{
'learning_rate': grid_learn, #default: .3
'max_depth': [1,2,4,6,8,10], #default 2
'n_estimators': grid_n_estimator,
'seed': grid_seed
}]
]
for model, param in tqdm(zip(vote_models, grid_param), total=len(vote_models)):
best_search = model_selection.GridSearchCV(estimator=model[1], param_grid=param, scoring='roc_auc')
best_search.fit(data_x_sample, data_y_sample)
best_param = best_search.best_params_
model[1].set_params(**best_param)
# グリッドサーチしたハイパーパラメータを使ったモデルで、投票モデルを学習
df_compare = pd.DataFrame(columns=['name', 'train_accuracy', 'valid_accuracy', 'time'])
scoring = ['accuracy']
vote_hard_model = ensemble.VotingClassifier(estimators=vote_models, voting='hard')
cv_rlts = model_selection.cross_validate(vote_hard_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
s = pd.Series(['hard', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='hard'+str(i))
df_compare = df_compare.append(s)
vote_soft_model = ensemble.VotingClassifier(estimators=vote_models , voting='soft')
cv_rlts = model_selection.cross_validate(vote_soft_model, data_x_sample, data_y_sample, cv=10, scoring=scoring)
for i in range(10):
s = pd.Series(['soft', cv_rlts['train_accuracy'][i], cv_rlts['test_accuracy'][i], cv_rlts['fit_time'][i]], index=df_compare.columns, name='soft'+str(i))
df_compare = df_compare.append(s)
plt.figure(figsize=(12,3))
sns.boxplot(data=df_compare, y='name', x='valid_accuracy', orient='h', color=base_color, linewidth=0.5, width=0.5)
plt.grid()
plt.show()
df_compare.groupby('name').mean().sort_values(by='valid_accuracy', ascending=False)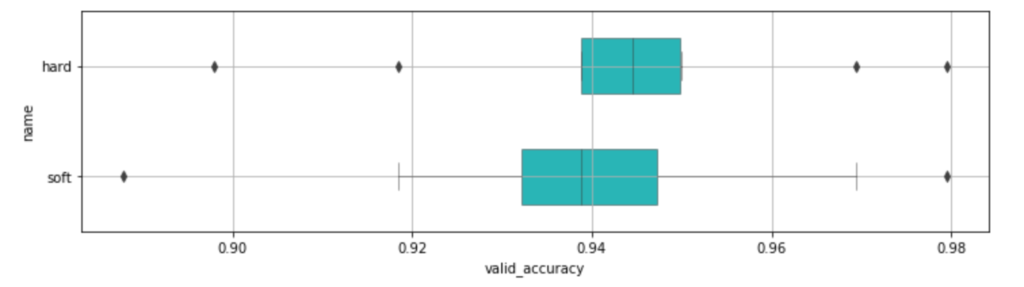
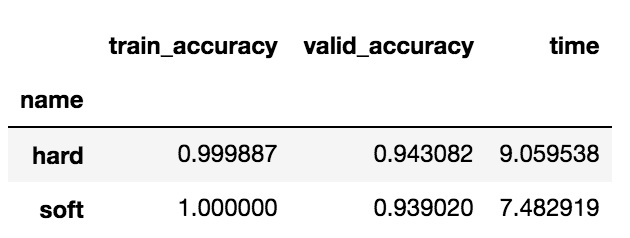
これはあまり効果はなさそうですね。
(valid_accuracyでソートしているので、先ほどのhardとsoftの行が逆になってしまっています)
この辺りは割と最後にわずかの数パーセント上がってくれないかな?くらいの気持ちだったりします。
精度によるモデル評価
改めて精度を確認してみます。
以下のように混合行列とROC曲線を可視化してみました。
train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3, random_state=0)
vote_soft_model.fit(train_x, train_y)
pred = vote_soft_model.predict(valid_x)
fig, axs = plt.subplots(ncols=2,figsize=(15,5))
sns.heatmap(metrics.confusion_matrix(valid_y, pred), vmin=0, annot=True, fmt='d', cmap=cm, ax=axs[0])
axs[0].set_xlabel('Predict')
axs[0].set_ylabel('Ground Truth')
axs[0].set_title('Accuracy: {}'.format(metrics.accuracy_score(valid_y, pred)))
fpr, tpr, thresholds = metrics.roc_curve(valid_y, pred)
axs[1].plot(fpr, tpr, color=base_color)
axs[1].set_title('ROC curve')
axs[1].set_xlabel('False Positive Rate')
axs[1].set_ylabel('True Positive Rate')
axs[1].grid(True)
plt.show()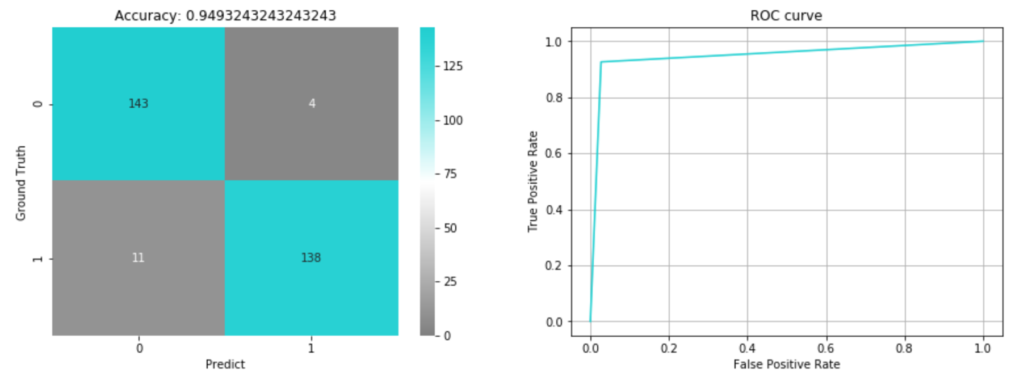
検証データに対する精度は0.949となりました。
ただし上記の検証データは、実際にはGround Truthが0のデータの方がたくさん存在する不均衡データですので、サンプリングで調整していた分を元に戻して混合行列を出してみます。
# 上記の結果を、実際の不均衡の比率に合わせた結果の混合行列
confusion_matrix = metrics.confusion_matrix(valid_y, pred)
confusion_matrix_scaled = np.array([
confusion_matrix[0, :]*(len(df[df['Class'] ==0])/sum(confusion_matrix[0, :])),
confusion_matrix[1, :]*(len(df[df['Class'] ==1])/sum(confusion_matrix[1, :])),
], dtype=np.int32)
plt.figure(figsize=(8,6))
sns.heatmap(confusion_matrix_scaled, vmin=0, annot=True, fmt='d', cmap=cm)
plt.xlabel('Predict')
plt.ylabel('Ground Truth')
plt.show()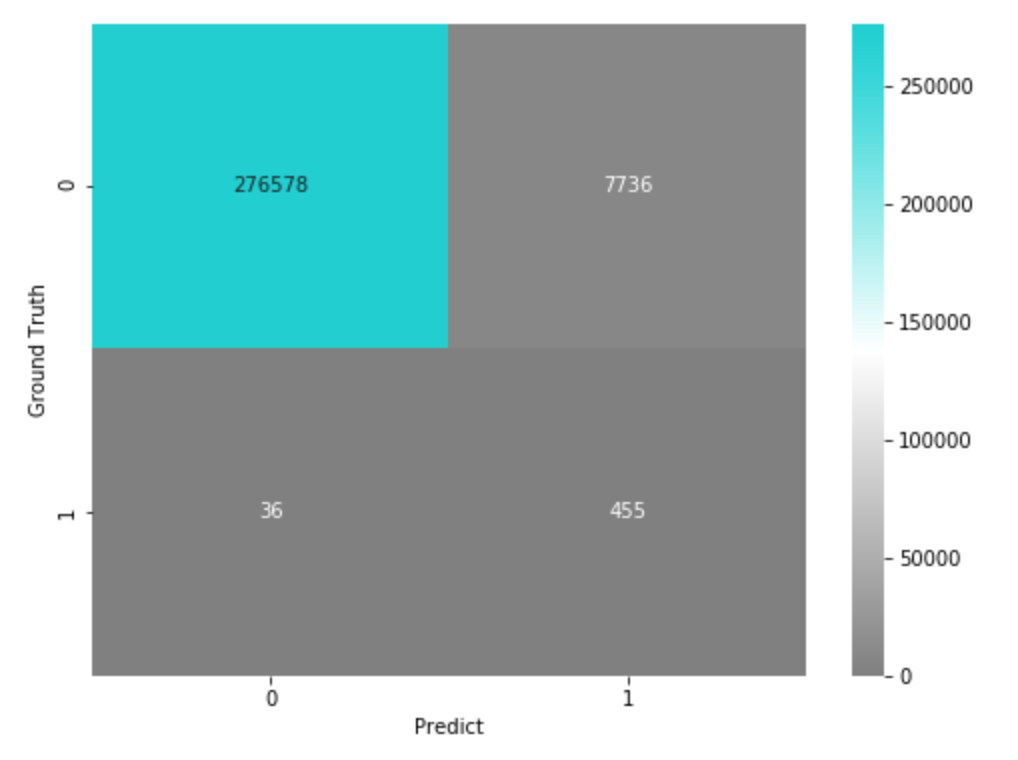
実際の運用時には、このくらいのFalse Positive・False Negativeが発生するという感じですね。
インパクトで見るモデル評価
今回は少し実務向けの設定を仮定した上で、それぞれの場合の損益の効果まで考えてみます。
クレジットカードといえば、盗難保険がついていますよね。
不正利用により顧客が失った金額は、こういった盗難保険などといった形でクレジットカード会社が負担するようになっているそうです。
ということは、不正利用がないと予測したけども実際に不正利用があった時には、不正利用を見逃したことになり、結果として顧客のお金は失われ、、その結果カード会社が負担するコスト\(cost_{fn}(account)\)が発生すると考えられます。
では仮に、実際に不正利用されたものを正しく不正利用だと予測できて、失うはずであった金額を抑えることが出来たと考えてみます。
これをいったん\(benefit_{tp}(account)\)と置いておきます。
逆に、不正利用があると予測したけども、実際に不正利用はなかった時には、そのアカウントに迷惑をかけることになり、利用停止を解除するコスト\(cost_{fp}(account)\)も発生すると考えてみます。
また、不正利用がないと予測して、実際に不正利用はない時の1アカウント当たりの平均利益\(benefit_{tn}(account)\)もいったん考えて置いておきましょう。
このようにして考えた場合に、損益行列は
| \(benefit_{tn}(True\:Negative\:accounts)\) | \(cost_{fp}(False\:Positive\:accounts)\) |
| \(cost_{fn}(False\:Negative\:accounts)\) | \(benefit_{tp}(True\:Positive\:accounts)\) |
と表せます。
ではさらに仮にですが、簡単な設定として、
- 利用停止を解除するコストとして、1アカウントあたり平均コスト1万円
- 不正利用を検知できず悪用されてしまった時の負担の、1アカウントあたり平均コスト100万円
としてみます。
本当は解除周りも人件費だったり、悪用されてしまった場合もカード再発行コストがあったりと、こんなにシンプルな話ではないと思いますが、簡単な設定としておきます。
そして\(benefit_{tn}\)、\(benefit_{tp}\)は、コストは防ぐことはできますが、利益自体は発生していませんので0とします。
そうすると、
- \(benefit_{tn}(account)=0\)
- \(cost_{fp}(account)=1{\times}account\)
- \(cost_{fn}(account)=100{\times}account\)
- \(benefit_{tp}(account)=0\)
と書けそうです。
この仮定で再度モデルが予測した時の最終的な損益行列は、
def benefit_tn(account):
return 0*account
def cost_fp(account):
return -1*account
# 不正利用を検知できずに悪用されてしまったと考える場合
def cost_fn(account):
return -100*account
def benefit_tp(account):
return 0*account
# 不正利用を未然に防ぐことができたと考える場合
def cost_fn2(account):
return 0*account
def benefit_tp2(account):
return 100*account
tn, fp, fn, tp = confusion_matrix_scaled.flatten()
fig, axs = plt.subplots(ncols=2, figsize=(14, 5))
bc_matrix = np.array([
[benefit_tn(tn), cost_fp(fp)],
[cost_fn(fn), benefit_tp(tp)],
], dtype=np.int)
sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[0])
axs[0].set_xlabel('Predict')
axs[0].set_ylabel('Ground Truth')
axs[0].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))
bc_matrix = np.array([
[benefit_tn(tn), cost_fp(fp)],
[cost_fn2(fn), benefit_tp2(tp)],
], dtype=np.int)
sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[1])
axs[1].set_xlabel('Predict')
axs[1].set_ylabel('Ground Truth')
axs[1].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))
plt.show()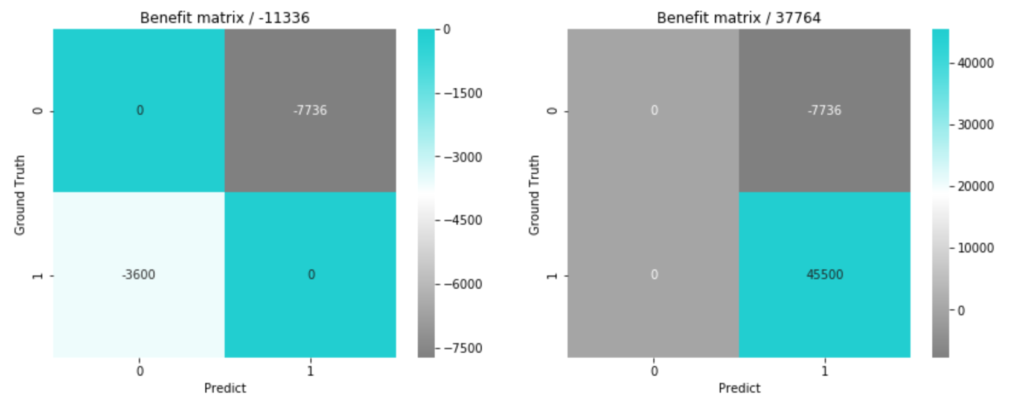
となりそうなことが分かりました。
predictでは予測確率が0.5以上でクラス判定としているので、この予測確率をどのくらいの閾値に設定しておけば、コストを最小化(利益を最大化)できるかを可視化してみます。
# 利益曲線を作る
pred_prob = vote_soft_model.predict_proba(valid_x)[:, 1] # 不正利用である確率
def get_expected_benefit(confusion_matrix):
confusion_matrix_scaled = np.array([
confusion_matrix[0, :]*(len(df[df['Class'] ==0])/sum(confusion_matrix[0, :])),
confusion_matrix[1, :]*(len(df[df['Class'] ==1])/sum(confusion_matrix[1, :])),
], dtype=np.int32)
tn, fp, fn, tp = confusion_matrix_scaled.flatten()
return benefit_tn(tn)+cost_fp(fp)+cost_fn(fn)+benefit_tp(tp)
thresholds = np.linspace(0, 1, 101)
benefits = np.zeros(len(thresholds))
for i, thresh in enumerate(thresholds):
pred_tmp = np.zeros((len(valid_y)))
pred_tmp[np.where(pred_prob > thresh)] = 1
confusion_matrix = metrics.confusion_matrix(valid_y, pred_tmp)
benefits[i] = get_expected_benefit(confusion_matrix)
plt.plot(thresholds, benefits, color=base_color)
plt.xlabel('Threshold')
plt.ylabel('Benefit')
plt.title('Benefit curve')
plt.grid()
plt.show()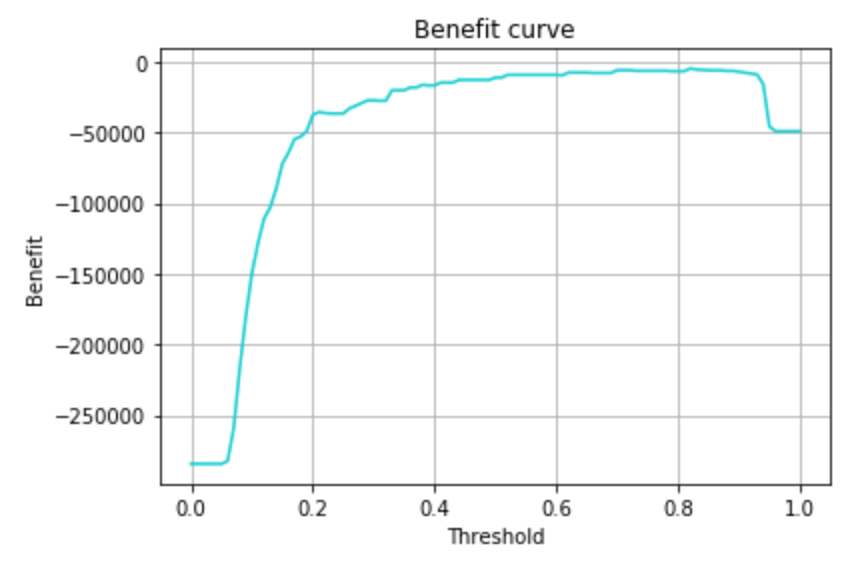
予測確率0.8あたりが最大になりそうですね。
学習データと検証データのセットを何パターンか試してみるため、何回かの検証データを使って信頼区間を出してみて、その上で最小コストとなる閾値を求めました。
trial_num = 20
thresholds = np.linspace(0, 1, 101)
benefits = np.zeros((trial_num, len(thresholds)))
for trial in tqdm(range(trial_num)):
train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3)
vote_soft_model.fit(train_x, train_y)
pred_prob = vote_soft_model.predict_proba(valid_x)[:, 1]
for i, thresh in enumerate(thresholds):
pred_tmp = np.zeros((len(valid_y)))
pred_tmp[np.where(pred_prob > thresh)] = 1
confusion_matrix = metrics.confusion_matrix(valid_y, pred_tmp)
benefits[trial, i] = get_expected_benefit(confusion_matrix)
plt.figure(figsize=(10,6))
lower_benefit, median_benefit, upper_benefit = mstats.mquantiles(benefits, [0.1, 0.5, 0.9], axis=0)
plt.plot(thresholds, median_benefit, color=base_color)
plt.fill_between(thresholds, upper_benefit, lower_benefit, color=base_color, alpha=0.3, linewidth=0)
max_benefit_point = thresholds[median_benefit == median_benefit.max()][0]
plt.vlines([max_benefit_point], benefits.min(), benefits.max(), color='black', linestyles='--')
plt.xlabel('Threshold')
plt.ylabel('Benefit')
plt.title('Benefit curve / interval 0.1--0.9')
plt.grid()
plt.show()
max_benefit_point0.8200000000000001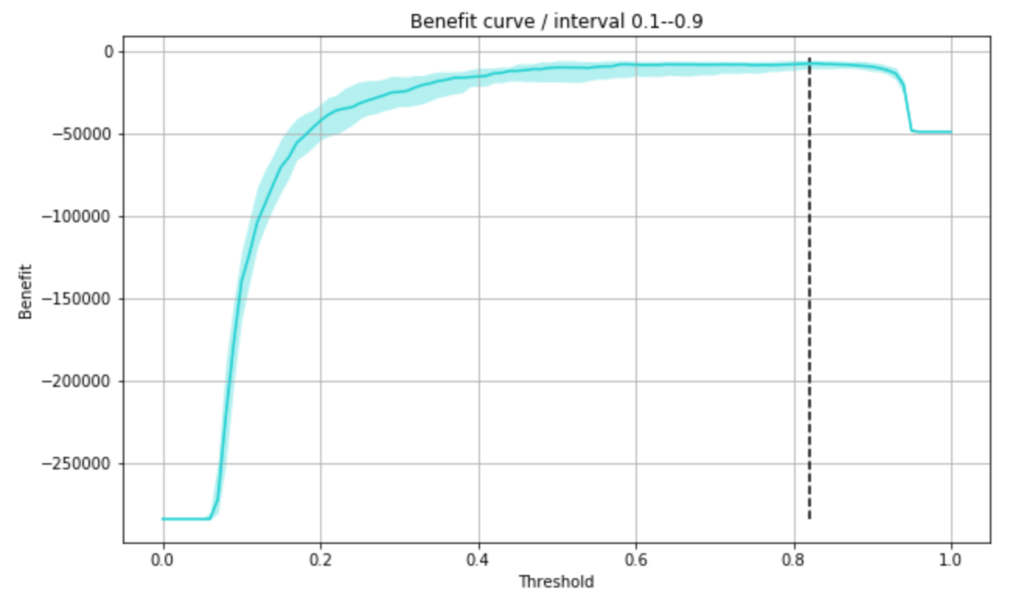
不正利用である確率が上記閾値を超えているものを不正利用と予測すれば、コストが最小になるとのことなので、この閾値で再度損益行列を出してみます。
# コストを最小化(利益を最大化)する閾値の時の損益行列
prob_thresh = 0.82
train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3, random_state=0)
vote_soft_model.fit(train_x, train_y)
pred_prob = vote_soft_model.predict_proba(valid_x)[:, 1]
pred = np.zeros((len(valid_y)))
pred[np.where(pred_prob > prob_thresh)] = 1
confusion_matrix = metrics.confusion_matrix(valid_y, pred)
confusion_matrix_scaled = np.array([
confusion_matrix[0, :]*(len(df[df['Class'] ==0])/sum(confusion_matrix[0, :])),
confusion_matrix[1, :]*(len(df[df['Class'] ==1])/sum(confusion_matrix[1, :])),
], dtype=np.int32)
tn, fp, fn, tp = confusion_matrix_scaled.flatten()
fig, axs = plt.subplots(ncols=2, figsize=(14, 5))
bc_matrix = np.array([
[benefit_tn(tn), cost_fp(fp)],
[cost_fn(fn), benefit_tp(tp)],
], dtype=np.int)
sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[0])
axs[0].set_xlabel('Predict')
axs[0].set_ylabel('Ground Truth')
axs[0].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))
bc_matrix = np.array([
[benefit_tn(tn), cost_fp(fp)],
[cost_fn2(fn), benefit_tp2(tp)],
], dtype=np.int)
sns.heatmap(bc_matrix, annot=True, fmt='d', cmap=cm, ax=axs[1])
axs[1].set_xlabel('Predict')
axs[1].set_ylabel('Ground Truth')
axs[1].set_title('Benefit matrix / {}'.format(bc_matrix.sum()))
plt.show()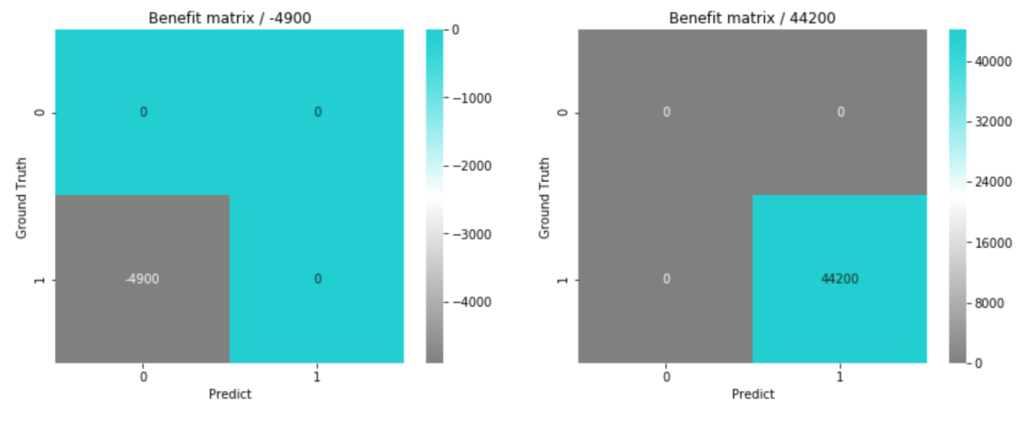
この仮定の場合においては、False Positiveを抑える(Precisionを高めにしておく)方が、コストがかからないということになりました。
おまけ
ついでに、今回のデータは主成分の元となる中身はどういうデータなのか分かりませんが、どの主成分がクラス判別に効きそうなのか、以下のように決定木モデルで主成分の傾向を分析してみました。
# 決定木による傾向分析
train_x, valid_x, train_y, valid_y = cross_validation.train_test_split(data_x_sample, data_y_sample, test_size=0.3, random_state=0)
decision_tree = tree.DecisionTreeClassifier()
decision_tree.fit(train_x, train_y)
dot_data = StringIO()
tree.export_graphviz(decision_tree, out_file=dot_data, feature_names=x_cols, max_depth=5)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_pdf('graph.pdf')
Image(graph.create_png())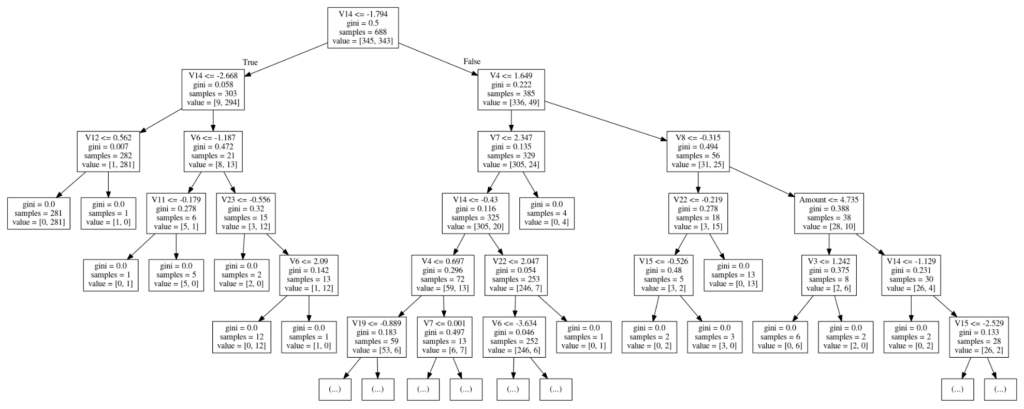
どうやら1つ目の切り分けルールでかなり分けられていることが、ジニ係数など確認してみて分かります。
そこで、データから1つ目ルールで切り分けられた集団ごとの不正予測の比率を確認してみます。
df_tmp = df.copy()
df_tmp.loc[df_tmp['V14'] <= -1.794, 'V14 <= -1.794'] = 1
df_tmp.loc[~(df_tmp['V14'] <= -1.794), 'V14 <= -1.794'] = 0
df_tmp['V14 <= -1.794'] = df_tmp['V14 <= -1.794'].astype(np.int)
g = sns.factorplot(x='V14 <= -1.794', y='Class',data=df_tmp, kind='bar', palette=[base_color2, base_color])
g = g.set_ylabels('Fraud Probability')
plt.hlines([df_tmp['Class'].sum()/len(df_tmp)], -1, 2, color='black', linestyles='--')
plt.show()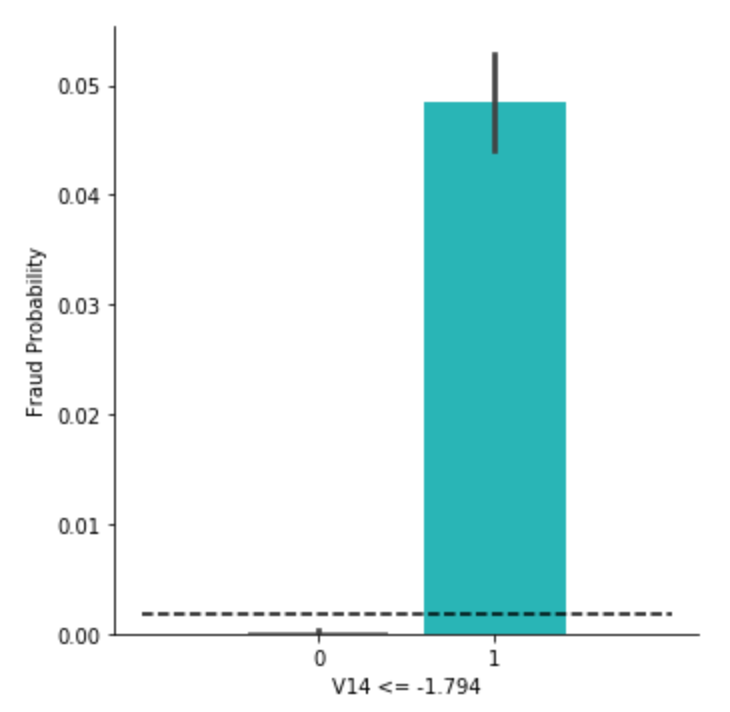
黒の点線が、もともとの全体における不正利用の確率0.00173を指しています。
可視化のように、ルールで切り分けられた集団ごとの確率で見ると、かなり異なることが分かりました。
ちゃんと値を出してみたものが以下。
df_tmp[df_tmp['V14 <= -1.794'] == 1]['Class'].sum()/len(df_tmp[df_tmp['V14 <= -1.794'] == 1])0.04848553345388788df_tmp[df_tmp['V14 <= -1.794'] == 0]['Class'].sum()/len(df_tmp[df_tmp['V14 <= -1.794'] == 0])0.00022829478292065125確かにこの主成分は、冒頭の相関行列でも他の成分に比べて絶対値が大きめでした。
意外と生データの段階において、不正利用かどうかを判断しやすいような項目があり、それが自然とこの主成分にまとめられたのかもしれません。
まとめ
以上、今回はビジネス意思決定者に対して、インパクトとしてのモデルの評価することを念頭に取り組んでみました。
損益行列のようなインパクト目線での効果を示すことで、意思決定者はモデルのビジネス経済的な効果を適切に理解し、より賢明な判断を下すことができるでしょう。
機械学習研究者などではなく、私のようにビジネスにおいてデータサイエンスを活用する立場の者であるのならば、こういったビジネスとして効果を把握し、モデルを活用することでこれだけの効果が得られますと示せるスキルも持ち合わせておくことが重要だと思います。
