この記事では、男子プロテニスプレイヤーのテーマを通じて、ベイズモデル分析の例をご紹介します。
具体的には、以下の参考図書で紹介されている『棋士の強さのモデリング』の分析を、テニスに応用してみる試みです。
上記書籍は、ベイズモデルの本の中でも具体的な問題設定とその実装例のコードが多く記載されており、動かしながら学習ができておすすめです。
なぜテニスなのか?は、私の趣味がテニスだからです。(週末プレイヤーですがちゃんと試合も出ます!)
プロテニスもよく観るので、親近感のあるテニスのデータで何かしらのスポーツアナリティクスをやってみたいなと思っていました。
(なので、たびたびテニスの専門用語などを普通に書いてしまうかと思います。読みづらくてすみません)
男子プロテニスプレイヤーの強さモデル
プロテニスの戦績データを用意しなければなりません。
今回は以下の通り、Kaggleのデータセットで男子プロテニスの試合結果データが公開されていましたので、これを使って各プレイヤーの強さをモデル化してみようと思います。
データの中身には、1試合ごとのツアー名、ツアーレベル、ツアー開催日、サーフェス、何回戦か、勝った選手の情報と得点情報、負けた選手の情報と得点情報などが格納されています。
データ加工のコードは省略しますが、一通りクリーニングを行い、かつ開催日tourney_dateから開催年yearだけ取得して別カラム化しておきました。
様々な得点情報がデータに含まれていますが、今回は
- 試合が開催された年
- その試合に勝ったプレイヤー
- 負けたプレイヤー
の情報だけで、各プレイヤーの強さを分析してみます。
前述の通り、今回は『棋士の強さのモデリング』で使われている以下のベイズ統計モデル
\(performance[g,1]{\sim}Normal(\mu[Loser],\sigma_{pf}[Loser]),\hspace{1em}g=1,{\ldots},G\)
\(performance[g,2]{\sim}Normal(\mu[Winner],\sigma_{pf}[Winner]),\hspace{1em}g=1,{\ldots},G\)
\(performance[g,1]<performance[g,2],\hspace{1em}g=1,{\ldots},G\)
\(\mu[n]{\sim}Normal(0,\sigma_{\mu}),\hspace{1em}n=1,{\ldots},N\)
\(\sigma_{pf}[n]{\sim}Gamma(10,10),\hspace{1em}n=1,{\ldots},N\)
を使ってみます。
考え方としては、
- \(Winner\) : 勝ったプレイヤーのインデックス
- \(Loser\) : 負けたプレイヤーのインデックス
とします。
各選手の強さを\(\mu[n]\)、勝負ムラを\(\sigma_{pf}[n]\)として、1回の勝負で発揮する力(パフォーマンス)は、平均\(\mu[n]\)、標準偏差\(\sigma_{pf}[n]\)の正規分布から生成されると考えます。
つまり、各選手はそれぞれ強さの値を持っているのですが、試合ごとに見れば、調子が良くてパフォーマンスを発揮できたという時もあれば、不調で本来の力を出すことができなかった時などがあり、その変化の大きさを力を発揮出来たりできなかったりの”ムラ”として考えます。
そして、勝負の結果はパフォーマンスの大小で決まる(大きかった方が勝つ)と考えます。
分析の対象の期間は、ひとまず直近のものを使うとして、2015年~2017年2月頃(データの最新期間)の戦績データを使います。
(2018年のデータまで欲しかったけど今は無いようです)
分析の対象選手は、この期間中の戦績データ数を確認しながら手動で選びます。
本当は世界ランキングTOP100位以内くらいの選手すべてでやってみたいところですが、処理が膨大になりますし、結果の解釈も難しくなるので、適当に数名選ぶことにします。
完全に個人的な興味とデータ数の兼ね合いで、以下のプレイヤーリストを用意しました。
ARR_TARGET_PLAYER = np.array([
'Roger Federer',
'Rafael Nadal',
'Novak Djokovic',
'Andy Murray',
'Stanislas Wawrinka',
'Juan Martin Del Potro',
'Milos Raonic',
'Kei Nishikori',
'Gael Monfils',
'Tomas Berdych',
'Jo Wilfried Tsonga',
'David Ferrer',
'Richard Gasquet',
'Marin Cilic',
'Grigor Dimitrov',
'Dominic Thiem',
'Nick Kyrgios',
'Alexander Zverev'
])やはりおなじみのBIG4(フェデラー、ナダル、ジョコビッチ、マレー)は外せません。(※以降敬称略)
ここに、錦織、デル・ポトロ、ラオニッチなどの中堅、ベルディヒ、ツォンガ、フェレールなど昔からTOP10周辺を位置するベテラン、そして最近活躍してきているティエム、キリオス、ズベレフなどの若手選手を入れてみました。
各プレイヤーの合計試合数と勝率は以下の通りです。
START_YEAR = 2015
# Use columns
df_matches = df_matches[["year", "winner_name", "loser_name"]]
# Convert data type
df_matches["year"] = df_matches["year"].astype(int)
df_matches["winner_name"] = df_matches["winner_name"].astype(str)
df_matches["loser_name"] = df_matches["loser_name"].astype(str)
# Extract target player records
df_matches = df_matches[
(df_matches['year'] >= START_YEAR) &
(df_matches['winner_name'].isin(ARR_TARGET_PLAYER)) &
(df_matches['loser_name'].isin(ARR_TARGET_PLAYER))
]
def plot_n_match_win_rate(df, arr_target_player):
"""Plot the number of matchs and win rates for each players.
Args:
df (pd.DataFrame): df_matches.
arr_target_player (np.ndarray): Target player list.
"""
arr_cnt = []
arr_rate = []
for player in arr_target_player:
cnt_win = len(df[df['winner_name'] == player])
cnt_lose = len(df[df['loser_name'] == player])
arr_cnt.append(cnt_win + cnt_lose)
arr_rate.append(cnt_win / (cnt_win + cnt_lose))
fig, axs = plt.subplots(ncols=2, figsize=(15, 5))
axs[0].bar(x=arr_target_player, height=arr_cnt, color='b', alpha=0.5)
axs[0].set(xlabel='player', ylabel='cnt')
for tick in axs[0].get_xticklabels():
tick.set_rotation(75)
axs[0].set_title("Plot the number of matches")
axs[1].bar(x=arr_target_player, height=arr_rate, color='r', alpha=0.5)
axs[1].set(xlabel='player', ylabel='rate')
for tick in axs[1].get_xticklabels():
tick.set_rotation(75)
axs[1].set_title("Plot the rate of win")
plt.show()
plot_n_match_win_rate(df_matches, ARR_TARGET_PLAYER)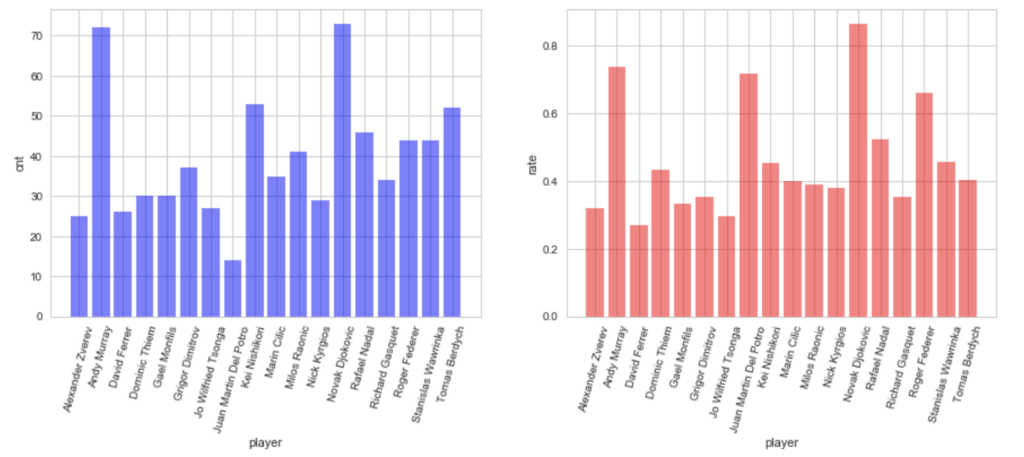
青が対象期間中の各選手の試合数(vs対象選手のみ)、赤が勝率になります。
ベイズモデリングといえども、データ数が少なすぎれば収束しない恐れがあり、デル・ポトロなどが若干データが少なめですが、収束しなかった時に外すとして、とりあえずこれで続行します。
上記の統計モデルに食わせるデータ形式を用意します。
def get_dict_target(arr_target):
"""Get dictionary of value of arr_target to number.
Args:
arr_target (np.ndarray): List.
Returns:
dic_target (dict[str, int]): Dictionary.
"""
dic_target = {}
for v in arr_target:
if v not in dic_target:
dic_target[v] = len(dic_target) + 1
return dic_target
def get_lw(df, arr_target_player, dic_target_player):
"""Get LW data for input model.
Args:
df (pd.DataFrame): df_matches.
arr_target_player (np.ndarray): Target player list.
dic_target_player (dict[str, int]): Dictionary of player to number.
Returns:
np.ndarray: LW array.
"""
LW = []
for player_a in arr_target_player:
for player_b in arr_target_player:
df_tmp = df[
(df['winner_name'] == player_a) &
(df['loser_name'] == player_b)
]
for _ in range(len(df_tmp)):
LW.append([dic_target_player[player_b], dic_target_player[player_a]])
df_tmp = df[
(df['winner_name'] == player_b) &
(df['loser_name'] == player_a)
]
for _ in range(len(df_tmp)):
LW.append([dic_target_player[player_a], dic_target_player[player_b]])
LW = np.array(LW, dtype=np.int32)
return LW
dic_target_player = get_dict_target(ARR_TARGET_PLAYER)
LW = get_lw(df_matches, ARR_TARGET_PLAYER, dic_target_player)上記のLWは「負け選手インデックス、勝ち選手インデックス」という順に、試合ごとに行を格納した2次元配列です。
これが後にパフォーマンスの大小を調整するためのデータになります。
さて、前述の統計モデルをStanで書いて学習させてみます。
def train_model(data, n_iter, n_chains):
"""Train the model.
Args:
data (dict[str, int or np.ndarray]): Input data.
n_iter (int): The number of iter.
n_chains (int): The number of chain.
Returns:
collections.OrderedDict: Result.
"""
model = """
data {
int N;
int G;
int<lower=1, upper=N> LW[G, 2];
}
parameters {
ordered[2] performance[G];
vector<lower=0>[N] mu;
real<lower=0> s_mu;
vector<lower=0>[N] s_pf;
}
model {
for (g in 1:G)
for (i in 1:2)
performance[g, i] ~ normal(mu[LW[g, i]], s_pf[LW[g, i]]);
mu ~ normal(0, s_mu);
s_pf ~ gamma(10, 10);
}
"""
fit = pystan.stan(model_code=model, data=data, iter=n_iter, chains=n_chains)
return fit.extract()
N_ITER = 1000
N_CHAINS = 4
data = {"N": len(dic_target_player), "G": len(LW), "LW": LW}
la = train_model(data, N_ITER, N_CHAINS)
上記コードのモデル部分のordered[2] performance[G];が今回のモデルで重要なところです。
ここが制約付きパラメータで1列目よりも2列目の方が大きいという制約を与えています。
したがってperformance[g, i] ~ normal(mu[LW[g, i]], s_pf[LW[g, i]]); で、LWの負けプレイヤーインデックスの方のパフォーマンスよりも、勝ちプレイヤーインデックスの方のパフォーマンスは大きくなるよう調整を行っているということになります。
ちなみに事前分布のガンマ分布は、プロットしてみれば分かりますが、正規分布などのような釣り鐘型の分布で、平均が1付近かつ正の値を取るような形状をしています。
正の値をとって、正規分布のような形をしてほしいという事前情報を与えたい時にこういった分布を用います。
処理を回してみたところ、Rhatがだいたいが1.00付近となり、いい感じに収束してくれていそうです。念のために、各チェインごとのサンプリングをプロットしてみた結果が以下になります。
def plot_chains_dist(arr_target_player, n_chains, la, target_param):
"""Plot distributions of each chains.
Args:
arr_target_player (np.ndarray): Target player list.
n_chains (int): The number of chains.
la (collections.OrderedDict): Result.
target_param (str): Target latest parameter.
"""
cmap = matplotlib.cm.get_cmap('tab10')
plt.figure(figsize=(10, 5))
for i, player in enumerate(arr_target_player):
for j in range(n_chains):
g = plt.violinplot(
la[target_param][j * 500:(j + 1) * 500, i],
positions=[i],
showmeans=False,
showextrema=False,
showmedians=False,
)
for pc in g['bodies']:
pc.set_facecolor(cmap(j))
plt.legend([f"chain {i + 1}" for i in range(n_chains)])
plt.xticks(list(range(len(arr_target_player))), arr_target_player)
plt.xticks(rotation=45)
plt.xlabel('player')
plt.ylabel(target_param)
plt.show()
plot_chains_dist(
arr_target_player=ARR_TARGET_PLAYER,
n_chains=N_CHAINS,
la=la,
target_param="mu",
)
plot_chains_dist(
arr_target_player=ARR_TARGET_PLAYER,
n_chains=N_CHAINS,
la=la,
target_param="s_pf",
)
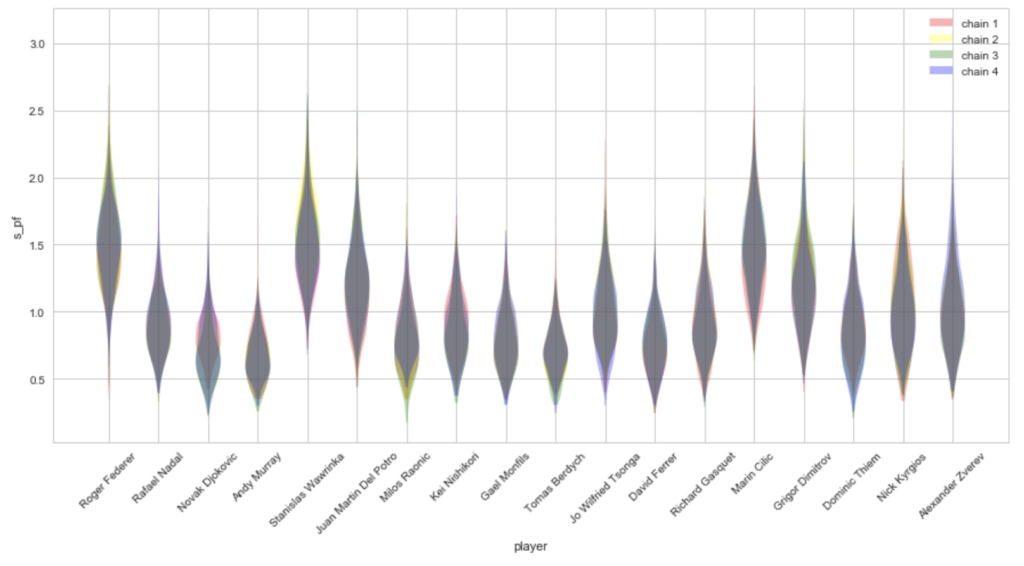
良い感じに重なってちゃんと収束していそうなので、ひとまずは問題なさそうです。
改めて統合したサンプリング結果をプロットしてみます。
まずは各選手の強さ\(\mu\)の事後分布が以下になります。
def plot_posterior_dist(arr_target_player, la, target_param):
"""Plot posterior distributeion of given latest parameter.
Args:
arr_target_player (np.ndarray): Target player list.
la (collections.OrderedDict): Result.
target_param (str): Target latest parameter.
"""
cmap = matplotlib.cm.get_cmap('tab10')
plt.figure(figsize=(15, 7))
for i, player in enumerate(arr_target_player):
g = plt.violinplot(
la[target_param][:, i],
positions=[i],
showmeans=False,
showextrema=True,
showmedians=True,
)
c = cmap(i % 10)
for pc in g['bodies']:
pc.set_facecolor(c)
g['cbars'].set_edgecolor(c)
g['cmaxes'].set_edgecolor(c)
g['cmedians'].set_edgecolor(c)
g['cmins'].set_edgecolor(c)
plt.xticks(list(range(len(arr_target_player))), arr_target_player)
plt.xticks(rotation=45)
plt.xlabel('player')
plt.ylabel(target_param)
plt.show()
def get_desc_posterior_dist(arr_target_player, n_chains, la, target_param):
"""Get summary of posterior distribution of given latest parameter.
Args:
arr_target_player (np.ndarray): Target player list.
n_chains (int): The number of chains.
la (collections.OrderedDict): Result.
target_param (str): Target latest parameter.
Returns:
pd.DataFrame: Dataframe of summary.
"""
summary = np.zeros((len(arr_target_player), n_chains))
for i, player in enumerate(arr_target_player):
samples = la[target_param][:, i]
median = np.median(samples, axis=0)
std = np.std(samples, ddof=1)
lower, upper = np.percentile(samples, q=[25.0, 75.0], axis=0)
summary[i] = [median, std, lower, upper]
df_summary = pd.DataFrame(
summary,
index=arr_target_player,
columns=['median', 'std', '25%', '75%'],
)
return df_summary
target_param = "mu"
plot_posterior_dist(
arr_target_player=ARR_TARGET_PLAYER,
la=la,
target_param=target_param,
)
df_s = get_desc_posterior_dist(
arr_target_player=ARR_TARGET_PLAYER,
n_chains=N_CHAINS,
la=la,
target_param=target_param,
)
display(df_s)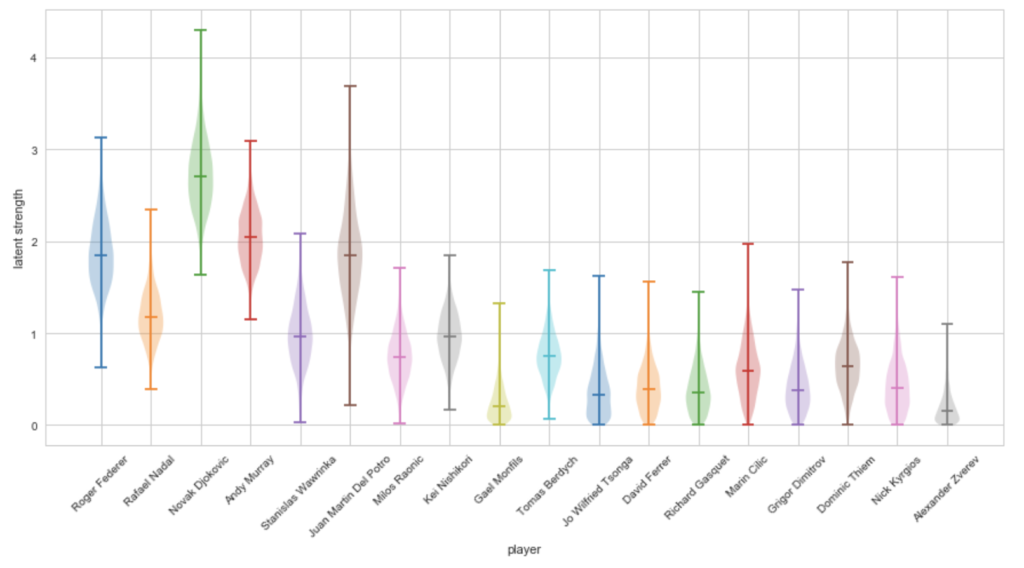
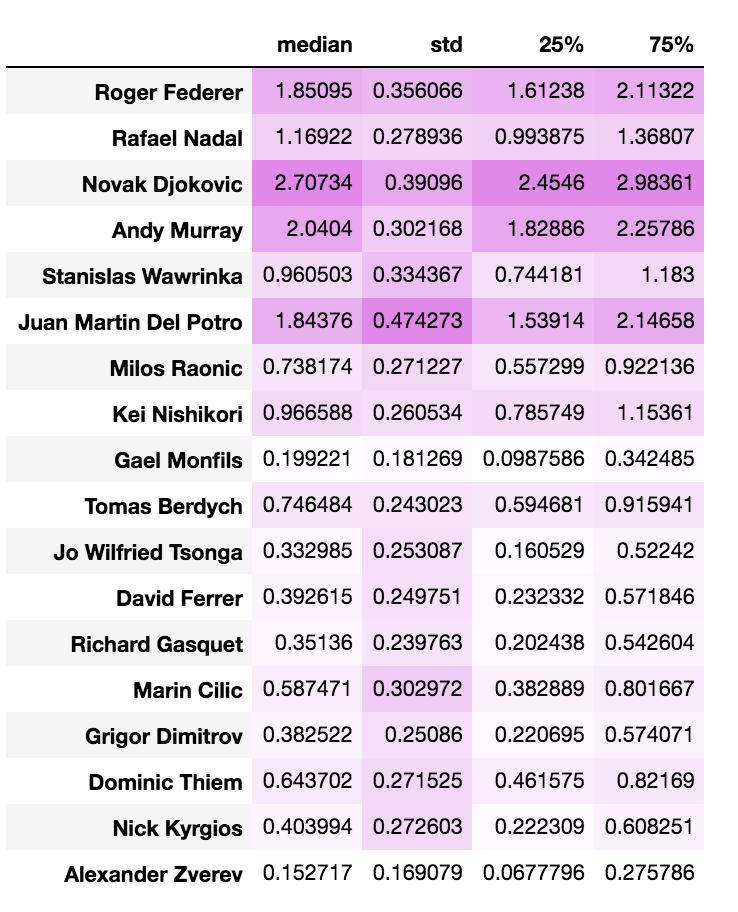
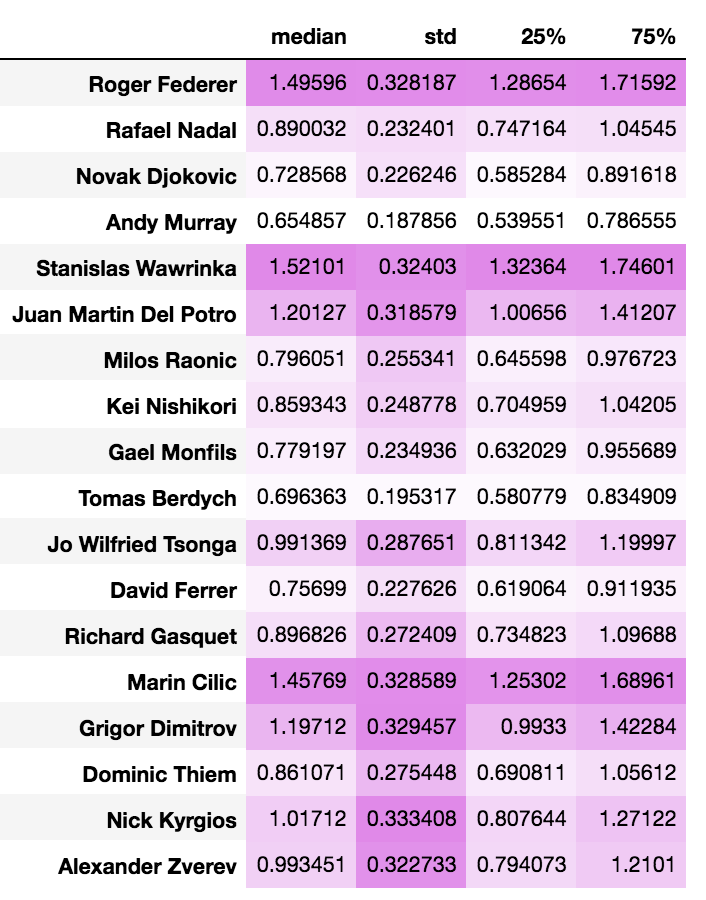
ヴァイオリンプロットが各選手の強さのプロット、表はそれぞれ中央値、不偏標準偏差、50%ベイズ信頼区間の下限、上限となっています。
対象期間がジョコビッチ1強時代であったため、ジョコビッチが1番強いと出ており、直感通りの結果となっています。
デル・ポトロもBIG4に引けを取らない強さとなっていますが、怪我などの影響で勝負回数が少ないからか、帯も大きく伸びていて不確実度が高いことが分かります。
個人的に意外だったのが、ワウリンカと錦織が同じくらいの強さとなっているところで、全然ワウリンカの方が強いと思っていました…。
対象期間中の戦績を可視化してみた結果が以下になります。
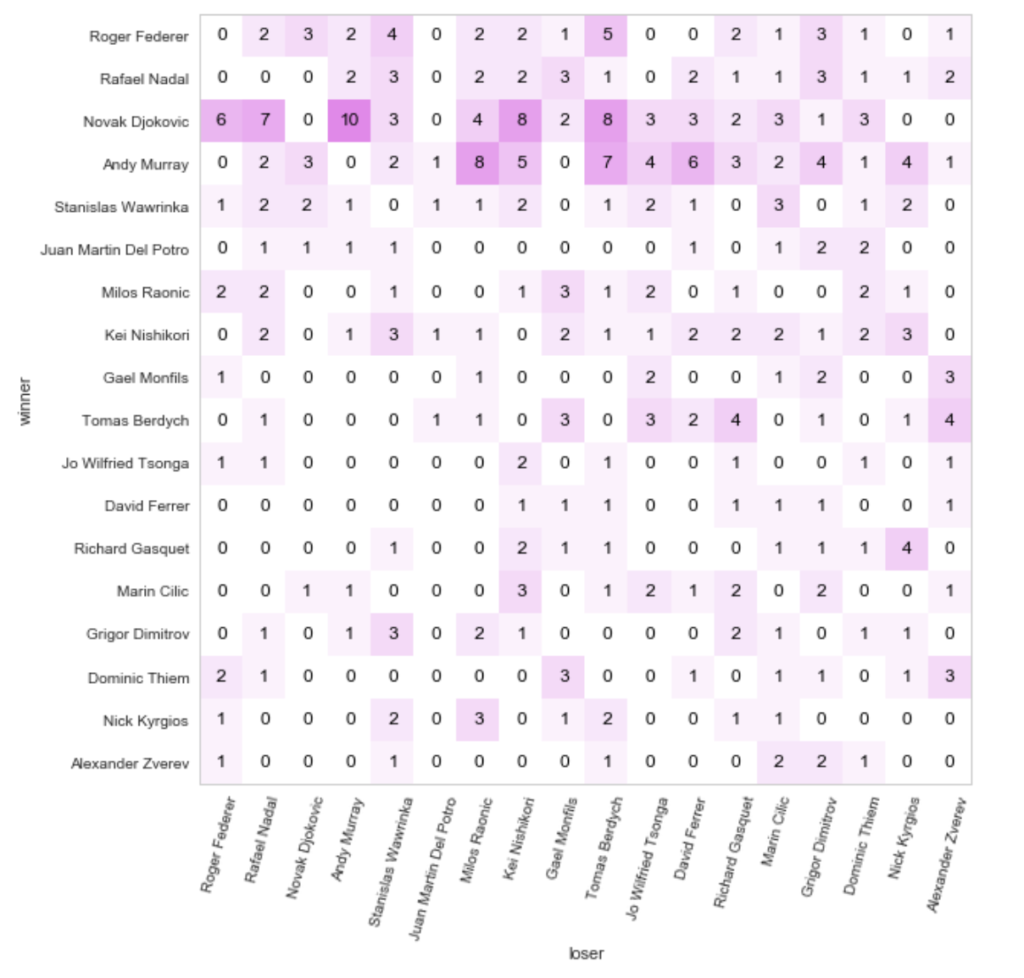
一気に確認できるようにしたかったため、あまりこのような可視化を行うことはないと思いますが、行が勝ちプレイヤー、列が負けプレイヤーであった試合が何回あったかをマス目の数値で表しました。
これを見ても確かに、この期間内では、錦織はワウリンカに3勝2敗で勝ち越しており、ワウリンカ、錦織共にBIG4にも勝ったりもしているため、改めて錦織選手がTOP10の中でもかなり強い部類に位置していることを認識できました。(今は怪我でランキングを落としてしまっていますが…)
また、対象期間中では、若手は中堅以上には若干劣っている様子で、その若手の中では、ティエムが強いとなっているようです。
ここはやはり2017年後半や2018年のデータが欲しいところ。
続いて、各選手の勝負ムラ\(\sigma_{pf}\)の事後分布が以下になります。
target_param = "s_pf"
plot_posterior_dist(
arr_target_player=ARR_TARGET_PLAYER,
la=la,
target_param=target_param,
)
df_s = get_desc_posterior_dist(
arr_target_player=ARR_TARGET_PLAYER,
n_chains=N_CHAINS,
la=la,
target_param=target_param,
)
display(df_s)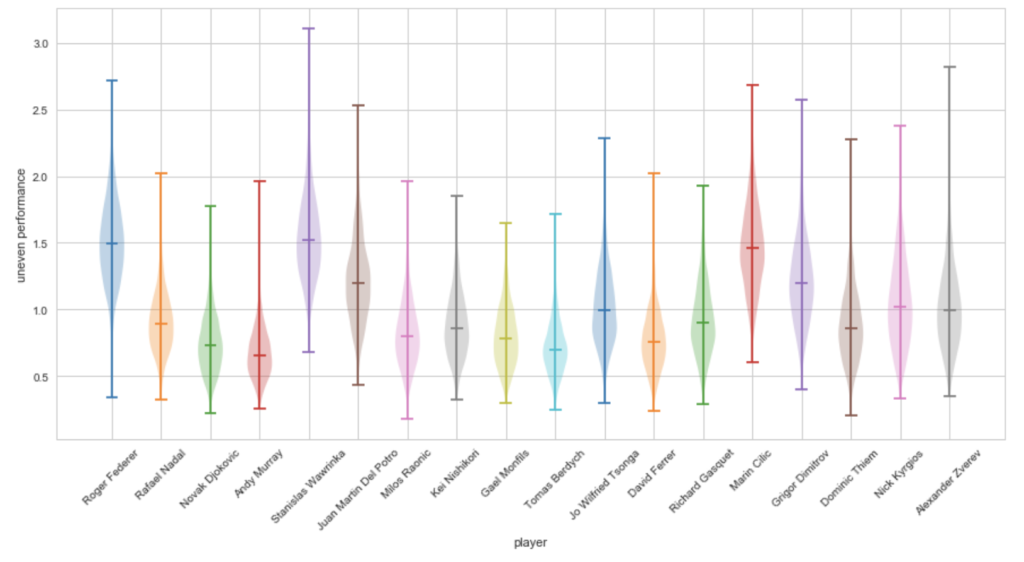
見たところ、ワウリンカが勝負ムラが一番大きいようです。
上記の戦績を見てみても、BIG4に限らず、同じ選手に勝ったり負けたりしていることがよくわかります。
BIG4の中では、この期間では、若干フェデラー、ナダルが勝ったり負けたりが多く、勝負ムラが少し大きめに出ました。
デル・ポトロは、マレー、ワウリンカに1勝1敗で、それ以外は安定して勝っていそうでしたが、なぜか大きめに出ました。
データ数が少なめだったからでしょうか、少し分かりません。
チリッチもこの期間は、ジョコビッチ、マレーに勝ったことがあり、その他選手とも勝ったり負けたりが多く、結果、勝負ムラが大きく出ています。
面白いなと思ったのが、若手選手が全体的に勝負ムラは少し高めに出ており、これはまだパフォーマンスを安定して発揮することに慣れていないということなのかなと思いました。
男子プロテニスプレイヤーの強さの時系列モデル
さて、前章では期間をある程度限定して分析を行いましたが、やはり時系列で各プレイヤーの強さがどのように推移してきているのかを見てみたいところです。
そこで先ほどの統計モデルをこちらで少し拡張してみました。
\(performance[y][g,1]{\sim}Normal({\mu}[Loser][y],\sigma_{pf}[Loser][y]),\hspace{1em}g=1,{\ldots},G,\hspace{0.5em}y=1,{\ldots},Y\)
\(performance[y][g,2]{\sim}Normal({\mu}[Winner][y],\sigma_{pf}[Winner][y]),\hspace{1em}g=1,{\ldots},G,\hspace{0.5em}y=1,{\ldots},Y\)
\(performance[y][g,1]<performance[y][g,2],\hspace{1em}g=1,{\ldots},G,\hspace{0.5em}y=1,{\ldots},Y\)
\({\mu}[n][1]{\sim}Normal(0,\sigma_{\mu}[n][1]),\hspace{1em}n=1,{\ldots},N\)
\({\mu}[n][y]{\sim}Normal({\mu}[n][y-1],\sigma_{\mu}[n][y-1]),\hspace{1em}n=1,{\ldots},N,\hspace{0.5em}y=2,{\ldots},Y\)
\(\sigma_{pf}[n][y]{\sim}Gamma(10,10),\hspace{1em}n=1,{\ldots},N,\hspace{0.5em}y=1,{\ldots},Y\)
\(\sigma_{\mu}[n][y]{\sim}Normal(0,1),\hspace{1em}n=1,{\ldots},N,\hspace{0.5em}y=1,{\ldots},Y\)
各プレイヤーの\(y\)年の強さを\({\mu}[n][y]\)、勝負ムラを\(\sigma_{pf}[n][y]\)とし、\(y\)年に行われる試合で発揮する力(パフォーマンス)は、平均\({\mu}[n][y]\)、標準偏差\(\sigma_{pf}[n][y]\)の正規分布から生成されると考えます。
そして、勝負の結果は同様にパフォーマンスの大小で決まる(大きかった方が勝つ)とします。
各選手のある年での強さ\({\mu}[n][y]\)は、その1つ前の年の強さ\(\mu[n][y-1]\)から生成されると考えます。
また、識別可能にするために、以下の仮定を入れます。
- 各選手の初年の強さは平均\(0\)、標準偏差\(\sigma_{\mu}[n][1]\)の半正規分布に従うとする
- 各選手の年別の強さの変化具合\(\sigma_{\mu}[n][y]\)は半正規分布に従うとする
2の仮定は、弱情報事前分布です。
無情報事前分布でも試してみましたが、うまく収束しませんでした。
といっても、次の年になると別人のようにいきなり強くなるということはあまり無いと思いますので、この程度の仮定はあっても大丈夫でしょう。
分析の対象期間は、2005年~2017年2月頃の戦績データとします。
この期間だと、前述で対象としていた若手選手などはほとんどデータが足りなくなりますので、改めて対象選手も手動で選択します。
分析対象選手は以下にしました。
ARR_TARGET_PLAYER = np.array([
'Roger Federer',
'Rafael Nadal',
'Novak Djokovic',
'Andy Murray',
'Stanislas Wawrinka',
'Juan Martin Del Potro',
'Kei Nishikori',
'Tomas Berdych',
'David Ferrer',
])前章同様に、対象期間の試合数と勝率の推移を可視化してみると以下のような感じです。
def plot_n_match_win_rate_ts(df, arr_target_year, arr_target_player):
"""Plot the number of matchs and win rates for each players on each years.
Args:
df (pd.DataFrame): df_matches.
arr_target_year (np.ndarray): Target year list.
arr_target_player (np.ndarray): Target player list.
"""
matrix_cnt = np.zeros((len(arr_target_year), len(arr_target_player)), dtype=np.float32)
matrix_rate = np.zeros((len(arr_target_year), len(arr_target_player)), dtype=np.float32)
for i, year in enumerate(arr_target_year):
for j, player in enumerate(arr_target_player):
cnt_win = len(df[(df['winner_name'] == player) & (df['year'] == year)])
cnt_lose = len(df[(df['loser_name'] == player) & (df['year'] == year)])
rate = 0 if (cnt_win + cnt_lose == 0) else cnt_win / (cnt_win + cnt_lose)
matrix_cnt[i, j] = cnt_win + cnt_lose
matrix_rate[i, j] = rate
for j, player in enumerate(arr_target_player):
if j % 3 == 0:
fig, axs = plt.subplots(ncols=3, figsize=(15, 3))
axs[j % 3].plot(arr_target_year, matrix_cnt[:, j], marker='o', color='b', alpha=0.5, label="match num")
axs[j % 3].set(title=player, xlabel='year', ylabel='cnt', ylim=[0, 40])
axs[j % 3].legend()
plt.show()
for j, player in enumerate(arr_target_player):
if j % 3 == 0:
fig, axs = plt.subplots(ncols=3, figsize=(15, 3))
axs[j % 3].plot(arr_target_year, matrix_rate[:, j], marker='o', color='r', alpha=0.5, label="win rate")
axs[j % 3].set(title=player, xlabel='year', ylabel='rate', ylim=[0, 1])
axs[j % 3].legend()
plt.show()
ARR_TARGET_YEAR = np.array(list(range(2005, 2017)))
plot_n_match_win_rate_ts(df_matches, ARR_TARGET_YEAR, ARR_TARGET_PLAYER)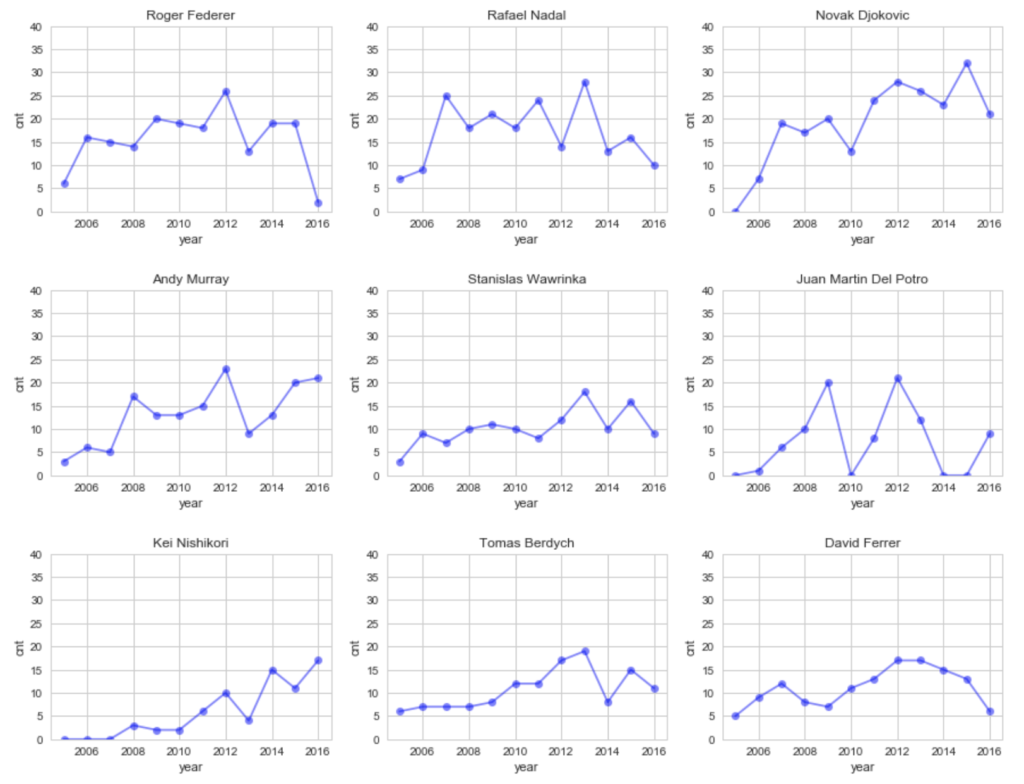
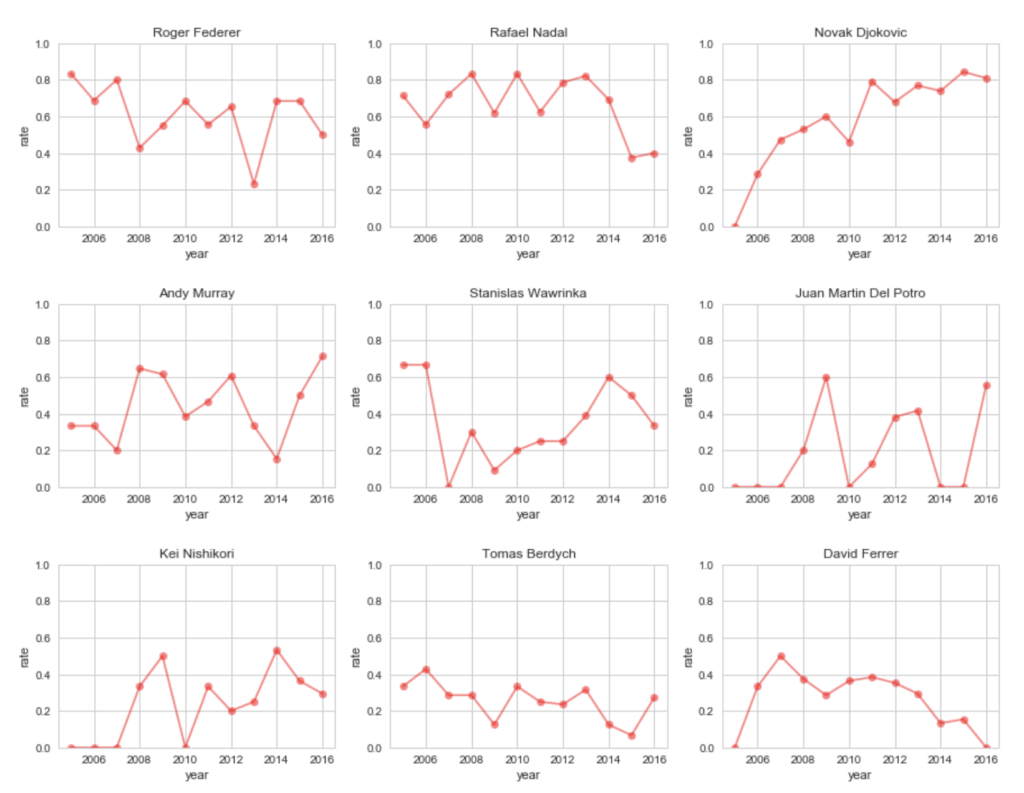
青が年ごとのその選手の試合数(vs対象選手)、赤が年ごとの勝率です。
全ての年で5試合以上くらいはありそうな選手と、やはり錦織選手を入れてみました。
次にモデルに入力するデータを作成してみます。
def get_lw_gy(df, arr_target_year, arr_target_player, dic_target_year, dic_target_player):
"""Get LW data and GY data for input model.
Args:
df (pd.DataFrame): df_matches.
arr_target_year (np.ndarray): Target year list.
arr_target_player (np.ndarray): Target player list.
dic_target_year (dict[int, int]): Dictionary of year to number.
dic_target_player (dict[str, int]): Dictionary of player to number.
Returns:
tuple[np.ndarray, np.ndarray]: LW array and GY array.
"""
LW = []
GY = []
for year in arr_target_year:
for player_a in arr_target_player:
for player_b in arr_target_player:
df_tmp = df[
(df['year'] == year) &
(df['winner_name'] == player_a) &
(df['loser_name'] == player_b)
]
for _ in range(len(df_tmp)):
LW.append([dic_target_player[player_b], dic_target_player[player_a]])
GY.append(dic_target_year[year])
df_tmp = df[
(df['year'] == year) &
(df['winner_name'] == player_b) &
(df['loser_name'] == player_a)
]
for _ in range(len(df_tmp)):
LW.append([dic_target_player[player_a], dic_target_player[player_b]])
GY.append(dic_target_year[year])
LW = np.array(LW, dtype=np.int32)
GY = np.array(GY, dtype=np.int32)
return LW, GY
dic_target_year = get_dict_target(ARR_TARGET_YEAR)
dic_target_player = get_dict_target(ARR_TARGET_PLAYER)
LW, GY = get_lw_gy(
df=df_matches,
arr_target_year=ARR_TARGET_YEAR,
arr_target_player=ARR_TARGET_PLAYER,
dic_target_year=dic_target_year,
dic_target_player=dic_target_player,
)LWは先程と同様で「負けプレイヤーインデックス、勝ちプレイヤーインデックス」が試合数分入っており、その試合番号に対応する年はいくつかというリストとしてGYを作成しています。
うまい人はもっと分かりやすく作るのでしょうけど、Stan力が足りなくてこうなってしまいました…
Stanでモデルを実装すると、以下のようになります。
def train_model_ts(data, n_iter, n_chains):
"""Train the model.
Args:
data (dict[str, int or np.ndarray]): Input data.
n_iter (int): The number of iter.
n_chains (int): The number of chains.
Returns:
collections.OrderedDict: Result.
"""
model = """
data {
int N;
int G;
int Y;
int<lower=1> GY[G];
int<lower=1, upper=N> LW[G, 2];
}
parameters {
ordered[2] performance[G];
matrix<lower=0>[N, Y] mu;
matrix<lower=0>[N, Y] s_mu;
matrix<lower=0>[N, Y] s_pf;
}
model {
for (g in 1:G)
for (i in 1:2)
performance[g, i] ~ normal(mu[LW[g, i], GY[g]], s_pf[LW[g, i], GY[g]]);
for (n in 1:N)
mu[n, 1] ~ normal(0, s_mu[n, 1]);
for (n in 1:N)
for (y in 2:Y)
mu[n, y] ~ normal(mu[n, y-1], s_mu[n, y]);
for (n in 1:N)
s_mu[n] ~ normal(0, 1);
for (n in 1:N)
s_pf[n] ~ gamma(10, 10);
}
"""
fit = pystan.stan(model_code=model, data=data, iter=n_iter, chains=n_chains)
return fit.extract()
data = {
'N': len(dic_target_player),
'G': len(LW),
'Y': len(dic_target_year),
'GY': GY,
'LW': LW,
}
la_ts = train_model_ts(data=data, n_iter=N_ITER, n_chains=N_CHAINS)
収束の確認などは省略しますが、大丈夫そうでした。
結果について可視化してみます。
まずは各プレイヤーの強さの時系列の推移をプロットしてみます。
def plot_posterior_dist_ts(arr_target_year, arr_target_player, la, target_param):
"""Plot posterior distributeion of given latest parameter on each years (time series).
Args:
arr_target_year (np.ndarray): Target year list.
arr_target_player (np.ndarray): Target player list.
la (collections.OrderedDict): Result.
target_param (str): Target latest parameter.
"""
cmap = matplotlib.cm.get_cmap('tab10')
plt.figure(figsize=(15, 7))
for j, player in enumerate(arr_target_player):
samples = la[target_param][:, j, :]
medians = np.median(samples, axis=0)
lower, upper = np.percentile(samples, q=[25.0, 75.0], axis=0)
c = cmap(j)
plt.plot(arr_target_year, medians, marker='o', label=player, color=c)
plt.fill_between(arr_target_year, lower, upper, alpha=0.2, color=c)
plt.xlabel('year')
plt.ylabel(target_param)
plt.legend(loc='lower left', bbox_to_anchor=(1, 0.5))
plt.title("Time series of estimated latent strength")
plt.show()
# Latent strength
plot_posterior_dist_ts(
arr_target_year=ARR_TARGET_YEAR,
arr_target_player=ARR_TARGET_PLAYER,
la=la_ts,
target_param="mu",
)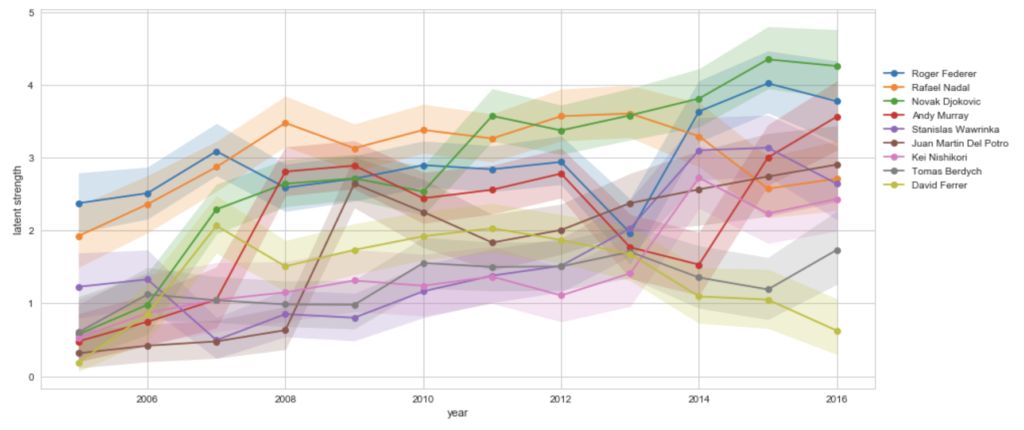
個人的には、割りと納得の推移結果となりました。
2005年頃は、やはりフェデラー、ナダルの2強時代であった様子がよくわかります。
そして、2008年頃から、フェデラー、ナダルに迫る若手、ジョコビッチ、マレー、デル・ポトロなどの強さが、やはり上位に推移してきていることがわかります。
錦織は2014年に強さが急激に上昇しており、この年に初めて世界ランクTOP10入りしました。
デル・ポトロは2009年(初めてグランドスラムに優勝した年)に急激に上昇するも、怪我の影響で推移を落としている様子が見えています。
マレーがかなりジグザグしていますが、2008年頃からフェデラー、ナダルに勝つようになり、この頃に世界ランク2位まで上り詰めるものの、2014年に怪我で不調となっていますので、そのような様子がはっきりと現れています。
ちなみに詳しいところはまだよく分かっていないのですが、この時系列では年内での強さの比較のため、年を跨いだ強さの比較はできないのかなと思います。
例えば、2007年のフェデラーよりも2008年のナダルの方が強そうな結果は出ていますが、2007年はフェデラーの方が多く勝った、2008年ではナダルの方が多く勝ったという結果から導いているはずなので、直接そこを比較しているわけではないと思います。
続いて、各プレイヤー・各年ごとの勝負ムラの事後分布について、可視化してみます。
def plot_posterior_dist_ts_ply(arr_target_year, arr_target_player, la, target_param):
"""Plot posterior distributeion of given latest parameter on each years.
Args:
arr_target_year (np.ndarray): Target year list.
arr_target_player (np.ndarray): Target player list.
la (collections.OrderedDict): Result.
target_param (str): Target latest parameter.
"""
cmap = matplotlib.cm.get_cmap('tab10')
for j, player in enumerate(arr_target_player):
if j % 3 == 0:
fig, axs = plt.subplots(ncols=3, figsize=(15, 3))
g = axs[j % 3].violinplot(
la[target_param][:, j, :],
positions=arr_target_year,
showmeans=False,
showextrema=False,
showmedians=False,
)
c = cmap(j%10)
for pc in g['bodies']:
pc.set_facecolor(c)
pc.set_alpha(0.7)
axs[j % 3].set(title=player, xlabel='year', ylabel=target_param)
plt.show()
# Uneven performance
plot_posterior_dist_ts_ply(
arr_target_year=ARR_TARGET_YEAR,
arr_target_player=ARR_TARGET_PLAYER,
la=la_ts,
target_param="s_pf",
)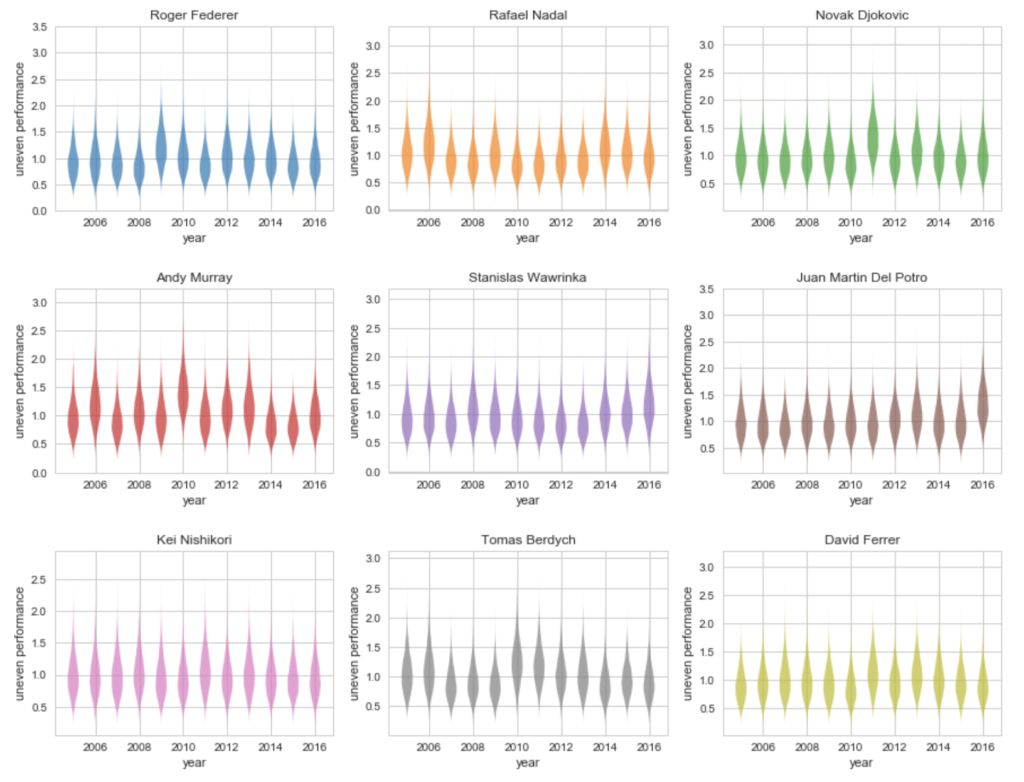
マレーが、年によって勝負ムラが大きくなるような結果となりました。
ワウリンカは、直近(2015〜2017.02)の分析では勝負ムラが大きかったものの、それまでの年で言えば、比較的大きくなかったようです。
ちょっと意外だったのが、錦織選手が、直近(2015〜2017.02)の分析と同様、各年においても勝負ムラはあまり大きくない傾向にあり、勝つ相手には勝つ、負ける相手には負けるがハッキリしているようです。
確かに対BIG4においても、ナダルには割りと勝つことが多い(ただしクレーは除く笑)印象があり、ジョコビッチには苦手意識を持っていそうな印象がありますが、どうなんでしょう。
最後に、各プレイヤー、各年ごとの成長の変化の度合いの事後分布を確認してみます。
# Change of strength
plot_posterior_dist_ts_ply(
arr_target_year=ARR_TARGET_YEAR,
arr_target_player=ARR_TARGET_PLAYER,
la=la_ts,
target_param="s_mu",
)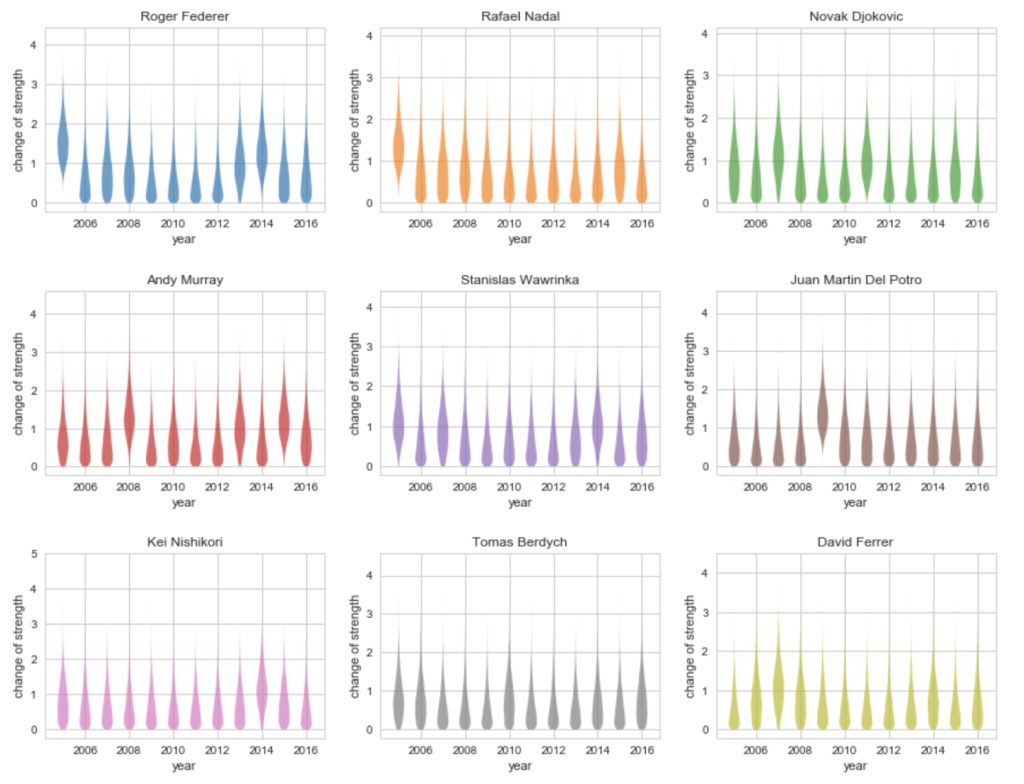
ここはやはり、基本的には、強さの時系列のモデルの傾きと、大きさが連動している様子が見られます。
初年の強さを 0 から推定させていることもあり、元から強かったフェデラー、ナダルがいきなり強くなっているように見えていますので、この辺りは無視した方が良さそうです。
マレーは、フェデラー、ナダルに勝つようになった上向きの強さの変化と、不調による下向きの強さの変化があったことが見て取れます。
他も強さの時系列と同様、デル・ポトロは、2009年で強さが大きく変化している、錦織は、2014年で強さが大きく変化していることがわかります。
まとめ
以上、今回はテニスプレイヤーの強さをベイズモデルで分析をしてみる例をご紹介しました。
感想として、結構ボリュームのある分析となり、長い記事になってしまいましたが、楽しかったです。
今回の分析だけでもまだやり残していることは多々あるように思います。
例えば、成長の変化の大きさは年齢に比例して小さくなる仮定を入れてみるとか、ただの勝敗だけでなくスコアの大きさを考慮に入れたらどうなるか、などです。
今回の方法は「勝ったか負けたか」という情報のみで、それらしい強さモデルを出すことができる点でとても強力な方法です。
前述で紹介した書籍内では他にも、アンケートの人気投票などで回答者にTOP3を回答してもらった場合などにも使えると述べられています。
その場合は、LWが「試合ごとの結果」だったのを「回答者ごとの結果」にして、制約付きパラメータをordered[3]とするイメージで分析が可能でしょう。
その他にも、例えば、競馬などのレース結果で、馬の強さをモデル化してみるとかも面白いかもしれません。
1〜5着までの結果を入力して、ordered[5]で分析すれば良いと思います。
このように応用先はいくらでも考えられる方法ですので、ぜひ皆さんも興味のある分野で試してみてはいかがでしょうか。
