近年において、深層学習は機械学習の中でも強力な手法ですが、一般的に予測や分類などのタスクにおいて確信度や不確実性を示すベイズ的なアウトプットを得ることは難しいです。
今回は、深層学習において、汎化性能を保つための工夫の一つであるDropoutを使って推論を行うことが、近似的にベイズ推論になっているという論文がありますので、それについて紹介します。
実は結構シンプルな方法でそれを実施することができ、実際に私も実務で使うことで「予測が難しい傾向にある教師データはこれらです」といったインサイトを得ることができ強力な方法でしたので、皆さんの学習の役に立てば幸いです。
Dropoutによる近似ベイズ推論
論文は下記になります。
- Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning: https://arxiv.org/abs/1506.02142
Dropoutを適用させた深層学習は、deep gaussian modelにおける変分ベイズ推論となる事を理論的に示しています。
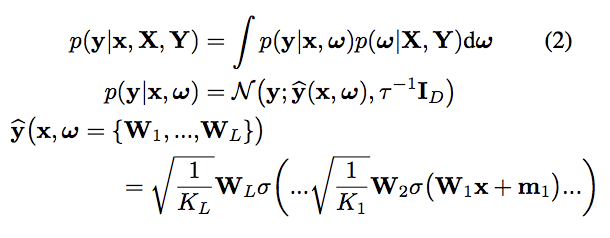
上記の\(p({\boldsymbol \omega}|\textbf{X}, \textbf{Y})\)事後分布を表しており、これを近似する分布\(q({\boldsymbol w})\)を
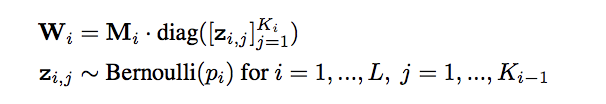
として考え、これがDropoutによってネットワークのユニットをランダムに0にすることと同じことを意味しています。
\(\textbf{y}\)の予測分布は以下のようにDropoutを適用したサンプリングの平均を取ることで得ます。
論文中ではこれをMonte Carlo dropout: MC dropout(モンテカルロ・ドロップアウト)と呼んでいます。
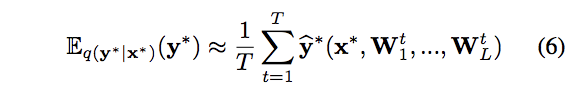
予測分布の不確実性(予測しにくさ)を表す指標として、論文では、分散あるいはエントロピーの利用が提言されています。
分散はMC dropoutで予測の分散を計算することができ、エントロピーも予測分布から一般的なエントロピーを計算させることができることを示しています。
予測分散:
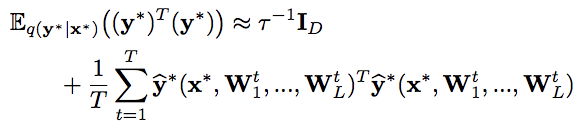
エントロピー:
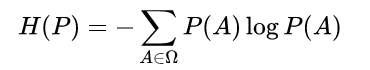
MNISTによる実証
それでは実際に、Dropoutを適用して深層学習モデルを学習し、Dropoutを適用したまま推論を繰り返して予測分布を作成してみます。
論文と同様に、MNIST画像分類タスクで実験的に行ってみます。
深層学習ライブラリはChainerを使いました。
MNISTのデータは下記のように準備します。
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import chainer
import chainer.functions as F
import chainer.links as L
from chainer.training import extensions
from PIL import Image
from tqdm import tqdm
train, valid = chainer.datasets.get_mnist()
train_x, train_y = train._datasets
valid_x, valid_y = valid._datasets
train_x = train_x.reshape(len(train_x), 1, 28, 28).astype(np.float32)
train_y = train_y.astype(np.int32)
valid_x = valid_x.reshape(len(valid_x), 1, 28, 28).astype(np.float32)
valid_y = valid_y.astype(np.int32)
train_dataset = chainer.datasets.tuple_dataset.TupleDataset(train_x, train_y)
valid_dataset = chainer.datasets.tuple_dataset.TupleDataset(valid_x, valid_y)
len(train_dataset), len(valid_dataset) # (60000, 10000)モデルのアーキテクチャは少しだけ畳み込みも追加して、以下のような簡単なCNNを作りました。
class Model(chainer.Chain):
def __init__(self):
super(Model, self).__init__()
with self.init_scope():
self.conv1 = L.Convolution2D(1, 16, 3)
self.conv2 = L.Convolution2D(16, 32, 3)
self.fc3 = L.Linear(None, 1000)
self.fc4 = L.Linear(1000, 1000)
self.fc5 = L.Linear(1000, 10)
def __call__(self, x, extract_feature=False):
h1 = F.max_pooling_2d(F.relu(self.conv1(x)), 2)
h2 = F.max_pooling_2d(F.relu(self.conv2(h1)), 2)
h3 = F.dropout(F.relu(self.fc3(h2)))
h4 = F.dropout(F.relu(self.fc4(h3)))
y = self.fc5(h4)
return yモデルを学習させます。
gpu = 0
model = L.Classifier(Model())
optimizer = chainer.optimizers.Adam(alpha=1e-4)
optimizer.setup(model)
if gpu >= 0:
chainer.cuda.get_device(gpu).use()
model.to_gpu(gpu)
epoch_num = 10
batch_size = 1000
train_iter = chainer.iterators.SerialIterator(train_dataset, batch_size)
test_iter = chainer.iterators.SerialIterator(valid_dataset, batch_size, repeat=False, shuffle=False)
updater = chainer.training.StandardUpdater(train_iter, optimizer, device=gpu)
trainer = chainer.training.Trainer(updater, (epoch_num, 'epoch'), out='tmp_result')
trainer.extend(extensions.Evaluator(test_iter, model, device=gpu))
trainer.extend(extensions.LogReport(trigger=(1, 'epoch')))
trainer.extend(extensions.LogReport())
trainer.extend(extensions.PrintReport(['epoch', 'main/loss', 'validation/main/loss', 'main/accuracy', 'validation/main/accuracy', 'elapsed_time']))
trainer.run()epoch main/loss validation/main/loss main/accuracy validation/main/accuracy elapsed_time
1 1.37316 0.418636 0.61555 0.8913 1.63919
2 0.396245 0.209561 0.883067 0.9406 3.01159
3 0.246652 0.147155 0.92705 0.957 4.12062
4 0.183742 0.115303 0.9449 0.9638 5.22699
5 0.149187 0.0943676 0.955483 0.9704 6.32683
6 0.124833 0.0795375 0.963017 0.9747 7.43109
7 0.110697 0.0700056 0.966367 0.9769 8.53159
8 0.0946027 0.0631644 0.971517 0.9789 9.63782
9 0.0862088 0.0572277 0.9735 0.9802 10.747
10 0.0797596 0.0533987 0.976167 0.9825 11.8497Chainerでは一般的にchainer.using_configでtrain中ではないと設定しDropoutを無効にして推定することが多いです。
これを意図的にtrain中としてDropoutを有効にします。
上記の概要の通り、1回の推論を行うことで、カテゴリカル分布の観測値を得ることができ、これをサンプリング回数繰り返し推論させることで、「結局どのラベルにどれだけ振り分けられたのか」といった多項分布の観測値を得ることができます。
これを平均を取ることで、一枚の画像につきどのラベルであるかを表す予測分布が得られることになります。
一枚の画像につき推論を繰り返した時に、全てのラベルに均等に振り分けられた場合、全てのラベルの確率が同じである一様分布ができます。
これは、その画像はどのラベルであるか検討がつかないという意味であり、つまり予測しにくい画像ということになります。
逆に予測しやすい画像を推論した結果として得られるサンプリングの分布は、どんなDropoutパターンでも予測ラベルが集中しやすいものになります。
上記の概要にも記した通り、この予測しにくさを定量化するため、今回はそれぞれの画像についてエントロピーを算出してみます。
エントロピーは、確率分布の予測しにくさを表します。
一般的に、確率分布が一様分布に従う時、エントロピーは最大になります。
以下は、バリデーションデータの中から、target_numのラベル番号に絞ってエントロピーを算出し、予測しやすいそのラベルの画像と、予測しにくいそのラベルの画像をプロットするコードを書いてみました。
model.to_cpu()
target_num = 0 # 試しに0の画像で検証してみる
sampling_num = 50
target_x = valid_x[np.where(valid_y == target_num)]
entropy = np.zeros((len(target_x)), dtype=np.float32)
for i in tqdm(range(len(target_x))):
x = target_x[i]
x = x[np.newaxis]
preds = np.zeros((sampling_num, 10), dtype=np.float32)
for j in range(sampling_num):
with chainer.using_config('train', True):
preds[j, :] = F.softmax(model.predictor(x), axis=1).data.squeeze()
preds = preds.mean(axis=0)
entropy[i] = np.sum(-preds*np.log(preds))
target_imgs = target_x.reshape(len(target_x), 28, 28)
target_imgs *= 255
target_imgs = target_imgs.astype(np.uint8)
high_entropy_imgs = target_imgs[np.argsort(entropy)[::-1][:30]]
low_entropy_imgs = target_imgs[np.argsort(entropy)[:30]]
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(low_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('low entropy top 30')
plt.show()
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(high_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('high entropy top 30')
plt.show()
予想通りの結果で、うまくいっていそうです。
バリデーションの中から0の画像で近似ベイズ推論で得られた予測分布のエントロピーが低かったもののTOP30画像、高かったもののTOP30画像を表示してみました。
エントロピーが低いものは予測がしやすい画像になりますので、とても綺麗でお手本のように書かれた0の画像が集まりました。
逆にエントロピーが高いものは予測がしにくく、他のラベルと間違えやすい画像ですので、形がいびつであったり汚い字が集まっています。
これを他の数字でも実行してみた結果が以下になります。
1の画像が以下の通り。

エントロピーが低いものは、ただ真っ直ぐに線が引かれているだけで、あまり面白くないかもしれないですが、間違いようがなさそうですね。
エントロピーが高いものに関しては、字がかすれていたり、線が太すぎても予測を間違えやすい傾向にあるようです。
2の画像が以下の通り。

エントロピーが高いものはかなりひどく、人でも読めなさそうなものも見受けられます。
3の画像が以下の通り。

エントロピーが低いものは、とても綺麗にバランスの取れたお手本のような3が集まりました。
エントロピーが高いものは読めないことは無さそうですが、やはりバランスが悪い字が多いです。
4の画像が以下の通り。

これもエントロピーが低いものはバランスが良くとても綺麗です。
以降、5~9までの画像を一気に記します。





以上のように、Dropoutを入れるだけなので様々な深層学習のネットワークアーキテクチャに適用することができ、結果も見ていて面白いです。
欠点があるとすれば、例えば、1つの入力につきサンプリング回数だけ推論を繰り返すことになるため、予測には少し計算に時間を要することなどあります。
また、予測がしにくいというデータは教えてくれますが、なぜ予測しにくいのか、どうすれば間違えにくくなるのかといった点は、やはり結果を見て自分で考察していく必要はありそうです。
このような方法を使った応用例として、オブジェクト検出のモデルにおいて、以下のような論文も出ています。
オブジェクト検出モデルに適用し、予測確率が高そうなバウンディングボックスを重ねて可視化しています。
- Dropout Sampling for Robust Object Detection in Open-Set Conditions: https://arxiv.org/abs/1710.06677
エントロピー算出に関する検証
この章では、私個人のちょっとした疑問に対する実験をやってみようと思います。
論文では、前回の記事のように具体的に計算は行っておらず、「カテゴリカル分布のパラメータが揺らぐので、それをエントロピーなり分散なりで計算すれば、深層学習の予測の不確実性を定量化できるだろう」と言っています。
この時、エントロピーを使ったとしても、定量化計算には例えば、
- 出力ベクトル→Softmax→平均値→エントロピー
- 出力ベクトル→平均値→Softmax→エントロピー
と算出してみると、どっちも問題なさそうな気がするのですが、どちらがより妥当なのかが疑問に思いました。
そこで、学習・予測データ、ドロップアウトなどの乱数を固定しておいて、両方の結果を見比べてみようと思います。
まずは前章と同じ、出力ベクトル→Softmax→平均値→エントロピーのパターンです。
モデルの出力値のソフトマックス関数の値について、モンテカルロドロップアウトサンプリングの平均値をとってエントロピーを計算させてみます。
コードは再掲になりますが、以下の通り。
target_num = 0 # 0の画像で実験
sampling_num = 50
target_x = valid_x[np.where(valid_y == target_num)]
entropy = np.zeros((len(target_x)), dtype=np.float32)
for i in tqdm(range(len(target_x))):
x = target_x[i]
x = x[np.newaxis]
preds = np.zeros((sampling_num, 10), dtype=np.float32)
for j in range(sampling_num):
with chainer.using_config('train', True):
preds[j, :] = F.softmax(model.predictor(x), axis=1).data.squeeze()
preds = preds.mean(axis=0)
entropy[i] = np.sum(-preds*np.log(preds))
target_imgs = target_x.reshape(len(target_x), 28, 28)
target_imgs *= 255
target_imgs = target_imgs.astype(np.uint8)
high_entropy_imgs = target_imgs[np.argsort(entropy)[::-1][:30]]
low_entropy_imgs = target_imgs[np.argsort(entropy)[:30]]
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(low_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('low entropy top 30')
plt.show()
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(high_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('high entropy top 30')
plt.show()
次に、出力ベクトル→平均値→Softmax→エントロピーのパターンです。
モデルの出力値のモンテカルロドロップアウトサンプリングの平均値について、ソフトマックス関数をとってエントロピー算出してみます。
コードを以下のように少し変更します。
target_num = 0
sampling_num = 50
target_x = valid_x[np.where(valid_y == target_num)]
entropy = np.zeros((len(target_x)), dtype=np.float32)
for i in tqdm(range(len(target_x))):
x = target_x[i]
x = x[np.newaxis]
preds = np.zeros((sampling_num, 10), dtype=np.float32)
for j in range(sampling_num):
with chainer.using_config('train', True):
preds[j, :] = model.predictor(x).data.squeeze()
preds = preds.mean(axis=0)[np.newaxis]
preds = F.softmax(preds, axis=1).data.squeeze()
entropy[i] = np.sum(-preds*np.log(preds))
target_imgs = target_x.reshape(len(target_x), 28, 28)
target_imgs *= 255
target_imgs = target_imgs.astype(np.uint8)
high_entropy_imgs = target_imgs[np.argsort(entropy)[::-1][:30]]
low_entropy_imgs = target_imgs[np.argsort(entropy)[:30]]
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(low_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('low entropy top 30')
plt.show()
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(high_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('high entropy top 30')
plt.show()
まず結果はやっぱり完全一致するわけではありませんね。
しかし、傾向はやはり同じようなものになるよう。
ではさらにですが、ドロップアウトなしの出力ベクトル→Softmax→エントロピーを計算させてみると、結果が以下になります。
target_num = 0
target_x = valid_x[np.where(valid_y == target_num)]
entropy = np.zeros((len(target_x)), dtype=np.float32)
for i in tqdm(range(len(target_x))):
x = target_x[i]
x = x[np.newaxis]
with chainer.using_config('train', False):
preds = F.softmax(model.predictor(x), axis=1).data.squeeze()
entropy[i] = np.sum(-preds*np.log(preds))
target_imgs = target_x.reshape(len(target_x), 28, 28)
target_imgs *= 255
target_imgs = target_imgs.astype(np.uint8)
high_entropy_imgs = target_imgs[np.argsort(entropy)[::-1][:30]]
low_entropy_imgs = target_imgs[np.argsort(entropy)[:30]]
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(low_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('low entropy top 30')
plt.show()
fig, axs = plt.subplots(ncols=10, nrows=3, figsize=(20, 5))
for i, img in enumerate(high_entropy_imgs):
img = Image.fromarray(img)
axs[i//10, i%10].imshow(img)
axs[i//10, i%10].axis('off')
plt.suptitle('high entropy top 30')
plt.show()
やっぱり傾向は同じになるのですね。
ということは、例えば目的が能動学習に用いるなどであれば、いずれの方法でも、似たような効力は得られそうな気がします。
モンテカルロドロップアウトサンプリングを導出することでベイズの枠組みとして考えられることは、論文で理論的に定式化していますので、モンテカルロドロップアウトサンプリングから予測分布を導出する形まで、数式的には納得がいく気がします。
まとめ
今回は、モンテカルロドロップアウトサンプリングを用いたベイズ深層学習について解説しました。
通常の深層学習では、確信度や不確実性をアウトプットすることが難しい課題がありますが、モンテカルロドロップアウトサンプリングを取り入れることで、ベイズ的な不確実性を推定する方法を学びました。
本記事でも少し触れていましたが、このような方法で予測の不確実さも表すことで、深層学習の予測自体がどの程度外しうるか、不得意なデータはどんなものか、能動学習でピックアップするべきデータはどれか、など様々な発展のアイデアが考えられます。
やり方自体はシンプルですので、ぜひ皆さんも身近な場面で応用してみるなど試してみて下さい。
