新型コロナウイルス(COVID-19)の感染者数が日々急速に増えています。
こういった感染症流行の状況変化に対して一歩でも先に対策を講じるために、今後の流行の流れを予測することはとても重要です。
そのためのツールとして、今回は、感染症の広がりを予測するモデルおよびその実装を紹介します。
具体的には、SIRモデルを用いて新型コロナウイルスの感染者数の予測を試みてみました。
SIRモデルは感染症流行の様子を表すために使われるモデルです。
このモデルを使って新型コロナウイルスの流行を予測し、最尤推定とベイズ推定の手法を用いてパラメータを推定してみます。
SIRモデル
SIRモデルは感染症の流行(拡大)の振る舞いを表すための決定論的なモデルで、感染症の進行と共に人口が「Susceptible(感染可能)」、「Infected(感染者)」、「Recovered(回復者)」の3つの状態に変化することを表します。
実は1927年から登場した歴史のあるモデルでもあります。
詳細は以下の通り。
主な活用領域はやはり、ある人々の集団の中でインフルエンザや麻疹などの感染者数がどのように流行っていき、やがて落ち着くのかといった、疫学的な関心が主流です。
一方で、一部ではTwitterなどのSNS上の流行がどのようにバズっていき、やがて落ち着くのかみたいなものの説明にも応用されることがあるみたいです。
最尤法によるパラメータ推定と予測
SIRモデルのパラメータの推定は、オーソドックスには最尤推定が用いられるようです。
まずはコロナ感染者数のデータから、SIRモデルのパラメータを最尤推定で求め、今後の流行の様子を推定してみることにします。
都道府県別のコロナ感染者数のデータは以下を利用しました。(2020/04/23時点)
実際に読み込むデータは上記リポジトリのうちのprefectures.csvです。
都道府県別に、感染者数、回復者数、死亡者数が時系列で格納されています。
このデータで、I=感染者数、R=回復者数+死亡者数として、最尤推定でパラメータを推定し、流行を予測してみます。
SIRモデルおよび尤度関数は、scipyのodeintやminimizeを使って、以下のように実装できます。
from scipy.integrate import odeint
from scipy.optimize import minimize
def sir(y, t, beta, gamma):
dydt1 = -beta * y[0] * y[1]
dydt2 = beta * y[0] * y[1] - gamma * y[1]
dydt3 = gamma * y[1]
return [dydt1, dydt2, dydt3]
def estimate(ini_state, beta, gamma):
y_hat = odeint(sir, ini_state, ts, args=(beta, gamma))
est = y_hat[0:int(t_max / dt):int(1 / dt)]
return est[:, 0], est[:, 1], est[:, 2]
def likelihood(params): # params = [beta, gamma]
_, I_est, R_est = estimate(ini_state, params[0], params[1])
return np.sum((I_est - I_obs)**2 + (R_est - R_obs)**2)例えば、東京都の感染者数のデータを使い、パラメータの初期値を設定して、以下のように最適化を実行すると、パラメータを推定することができます。
df_tmp = df_covid.copy()
df_tmp['I'] = df_tmp['confirmed']
df_tmp['R'] = df_tmp['recovered'] + df_tmp['dead']
target_pref_en = 'Tokyo'
target_pref_name = pref_dic[target_pref_en] # 東京都
I_obs = df_tmp[df_tmp['pref_name'] == target_pref_name]['I'].astype(int).values
R_obs = df_tmp[df_tmp['pref_name'] == target_pref_name]['R'].astype(int).values
dates = df_tmp[df_tmp['pref_name'] == target_pref_name]['date']
N = int((I_obs[-1] + R_obs[-1]) * 1.5)
S0, I0, R0 = int(N - I_obs[0] - R_obs[0]), int(I_obs[0]), int(R_obs[0])
ini_state = [S0, I0, R0]
beta, gamma = 1e-6, 1e-3
mnmz = minimize(likelihood, [beta, gamma], method="nelder-mead") # Optimize logscale likelihood function
mnmz final_simplex: (array([[1.78169209e-05, 1.88211512e-02],
[1.78169392e-05, 1.88212536e-02],
[1.78169402e-05, 1.88212265e-02]]), array([2133869.22549074, 2133869.22549226, 2133869.22551036]))
fun: 2133869.225490737
message: 'Optimization terminated successfully.'
nfev: 134
nit: 71
status: 0
success: True
x: array([1.78169209e-05, 1.88211512e-02])x[0]が感染率、x[1]が除去率です。
実際のデータおよび推定されたパラメータを使って、その後の流行(感染者数の推移)を可視化すると、以下のようになりました。
n_pred = 50
t_max = len(I_obs) + n_pred
ts = np.arange(0, t_max, dt)
dates = dates.tolist()
d = dates[-1]
for _ in range(n_pred):
d = d + datetime.timedelta(days=1)
dates.append(d)
plt.figure(figsize=(10, 5))
plt.plot(dates, list(I_obs) + [None] * n_pred, "o", color="red",label="Infected (observation)")
plt.plot(dates, list(R_obs) + [None] * n_pred, "o", color="green",label="Removed (observation)")
_, I_est, R_est = estimate(ini_state, mnmz.x[0], mnmz.x[1])
plt.plot(dates, I_est, color="red", alpha=0.5, label="Infected (estimation)")
plt.plot(dates, R_est, color="green", alpha=0.5, label="Removed (estimation)")
plt.ylabel('Population')
plt.title('Prediction of Covid-19 epidemic in ' + target_pref_en)
plt.grid()
plt.legend()
plt.show()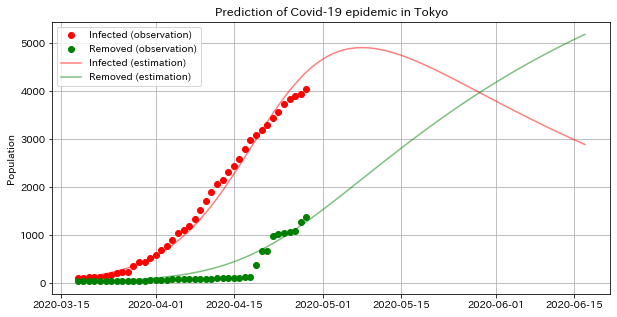
推定結果によれば、GWを開けてすぐには感染者数の上昇はピークに達し、その後緩やかに流行は収まっていくという結果になっています。
本当でしょうか…?
ベイズモデルによるパラメータ推定と予測
次に本命としてやってみたかったこと、ベイズでSIRモデルを表現してみて、感染率、除去率、予測の事後分布を推定してみます。
以下の論文が似たようなことに挑戦していたので、これを真似してみました。
- Contemporary statistical inference for infectious disease models using Stan: https://arxiv.org/abs/1903.00423
Stanではintegrate_ode関数で微分方程式の計算を表すことができるようです。
これに則って、感染者数、除去者数がポアソン分布に従って発生するとして、以下のようなモデルを書いてみました。
model_code = """
functions {
real[] sir(
real t,
real[] y,
real[] theta,
real[] x_r,
int[] x_i
) {
real dydt[3];
dydt[1] <- - theta[1] * y[1] * y[2];
dydt[2] <- theta[1] * y[1] * y[2] - theta[2] * y[2];
dydt[3] <- theta[2] * y[2];
return dydt;
}
}
data {
int T;
int T_pred;
real Y0[3];
int I_obs[T];
int R_obs[T];
real T0;
real TS[T+T_pred];
}
transformed data {
real x_r[0];
int x_i[0];
}
parameters {
real beta;
real gamma;
}
transformed parameters {
real y_hat[T+T_pred, 3];
real theta[2];
theta[1] = beta;
theta[2] = gamma;
y_hat <- integrate_ode(sir, Y0, T0, TS, theta, x_r, x_i);
}
model {
real lambda_i[T];
real lambda_r[T];
theta[1] ~ normal(1e-6, 1e-3);
theta[2] ~ normal(1e-3 ,1e-3);
for (t in 1:T) {
lambda_i[t] = y_hat[t ,2];
lambda_r[t] = y_hat[t, 3];
}
I_obs ~ poisson(lambda_i);
R_obs ~ poisson(lambda_r);
}
"""これをMCMCで解いて、y_hat, beta, gammaから予測、感染率、除去率のサンプリング結果を得ます。
例えば、東京・大阪・福岡・愛知の4つの都道府県で、それぞれベイズ推定を行い、得られたパラメータで今後の流行予測を可視化をしてみるコードと、結果が以下の通りになります。
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(20, 10))
axs = axs.flatten()
for i, target_pref_en in enumerate(['Tokyo', 'Osaka', 'Aichi', 'Fukuoka']):
target_pref_name = pref_dic[target_pref_en]
I_obs = df_tmp[df_tmp['pref_name'] == target_pref_name]['I'].astype(int).values
R_obs = df_tmp[df_tmp['pref_name'] == target_pref_name]['R'].astype(int).values
dates = df_tmp[df_tmp['pref_name'] == target_pref_name]['date']
N = int((I_obs[-1] + R_obs[-1]) * 1.5)
S0, I0, R0 = int(N - I_obs[0] - R_obs[0]), int(I_obs[0]), int(R_obs[0])
ini_state = [S0, I0, R0]
n_pred = 50
t_max = len(I_obs) + n_pred
dates = dates.tolist()
d = dates[-1]
for _ in range(n_pred):
d = d + datetime.timedelta(days=1)
dates.append(d)
ts = np.arange(0, t_max, 1)
data = {
'T': len(I_obs) - 1,
'T_pred': n_pred,
'Y0': ini_state,
'I_obs': I_obs[1:],
'R_obs': R_obs[1:],
'T0': ts[0],
'TS': ts[1:],
}
model = pystan.StanModel(model_code=model_code)
fit = model.sampling(
data=data,
iter=15000,
warmup=5000,
thin=50,
chains=3,
seed=19,
)
fit_dic = fit.extract()
x = dates[1:]
axs[i].plot(x, list(I_obs[1:]) + [None] * n_pred, marker='o', color='r', linestyle='None', label='Infected (observation)')
axs[i].plot(x, list(R_obs[1:]) + [None] * n_pred, marker='o', color='g', linestyle='None', label='Removed (observation)')
I_samples = fit_dic['y_hat'][:, :, 1]
medians = np.median(I_samples, axis=0)
lower, upper = np.percentile(I_samples, q=[25.0, 75.0], axis=0)
axs[i].plot(x, medians, color='r', alpha=0.5, label='Infected (estimation)')
axs[i].fill_between(x, lower, upper, color='r', alpha=0.2)
R_samples = fit_dic['y_hat'][:, :, 2]
medians = np.median(R_samples, axis=0)
lower, upper = np.percentile(R_samples, q=[25.0, 75.0], axis=0)
axs[i].plot(x, medians, color='g', alpha=0.5, label='Removed (estimation)')
axs[i].fill_between(x, lower, upper, color='g', alpha=0.2)
axs[i].set_ylabel('Population')
axs[i].set_title('Prediction of Covid-19 epidemic in ' + target_pref_en)
axs[i].grid()
axs[i].legend()
plt.show()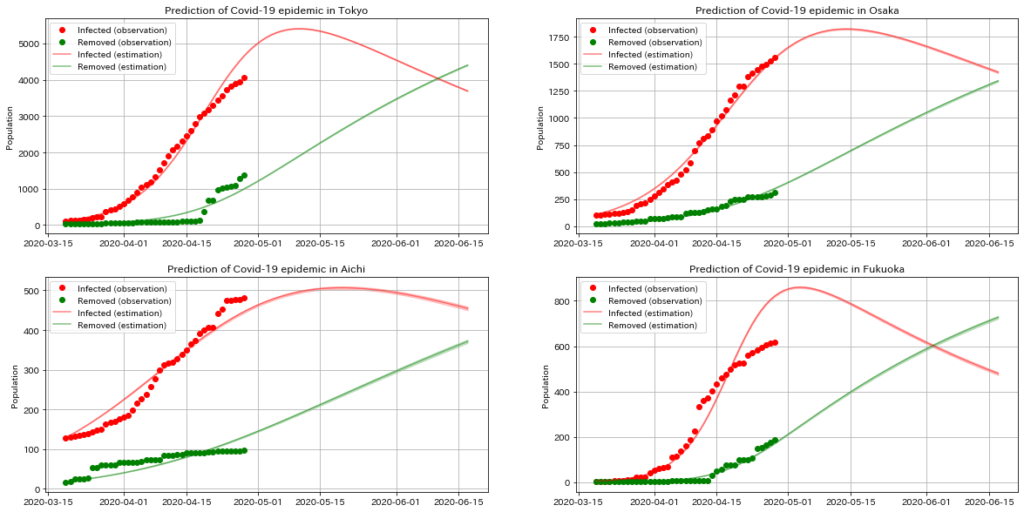
東京や大阪に関しては、データ数も多く、そもそも報告の結果も滑らかになっていたためか、とてもフィットしているように見えます。
最尤推定の時の結果と同様に、東京および大阪は、ゴールデンウィークを開けてすぐの頃にピークに達した後に、徐々に収束に向かうような感じになりました。
愛知、福岡に関しては、そもそもあまりフィットしていなさそうです。
このモデル自体に、表現する振る舞いに強い条件がついていそうな気がします。
コードは省略しますが、今度はデータが取れている都道府県すべてに対してベイズ推定を実施し、回復率・除去率の事後分布を可視化したものが以下になります。

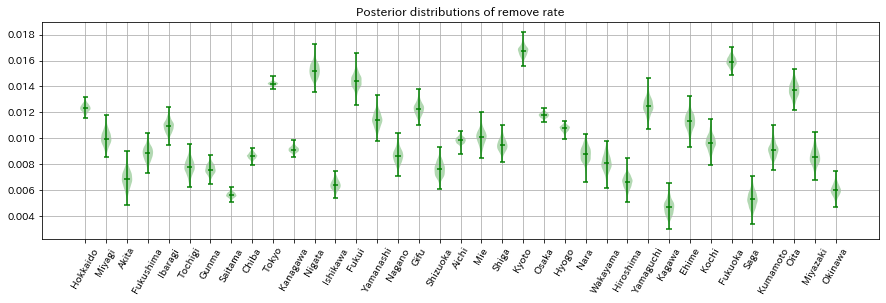
感染率が高いと推定されている都道府県は、事後分布の帯も広い傾向にあります。
調べてみるとデータ数も少し少なめで信頼性の観点で懸念はありそうです。
逆に、人数が多い都道府県の感染率が低いという傾向が見られます。
S自体を入力しているわけではないのですが、ちゃんとこの辺りの人数に関係して推定しているのかもしれません。
除去率に関しては、確かにデータを見てても感じましたが、東京が、人数や感染者数に対してあまり除去されていない感じであり、結果としてパラメータも相対的に低めに推定されたのかなと思います。
まとめ
今回は、SIRモデル x 最尤推定とベイズ推定を用いて、新型コロナウイルスの感染者数の予測を試みました。
Pythonを使用して実装したコードとその結果も紹介しましたが、皆様もぜひ手を動かしてみて、自身の知識を深めていただければと思います。
感染症の拡大予測は不確かな要素が多く含まれますが、それでもなお、予測モデルを通じて得られる洞察は、我々が理解し、適切な対策を講じる上で重要なものとなると思います。
最後に、私たち一人一人が行動を変えることが、全体の感染者数を抑える上で最も重要な要素であることを忘れないようにしましょう。
一日も早い終息を願います。
