機械学習の解釈手法SHAPのご紹介

この記事は約12分で読めます。

機械学習の進化は、私たちの生活に大きな影響を与えてきました。

しかし、複雑なモデルを扱う場合、その予測の仕組みを理解することは困難なことがあります。
そこで、解釈可能性(Interpretablity)の重要性がますます高まっています。
機械学習モデルが実際にどの特徴量がどうだったからどう予測したのかを知ることは、信頼性や説明責任を担保し、より洞察を得るために必要です。

このような背景から、近年注目を集めているのがSHapley Additive exPlanations: SHAPと呼ばれる解釈手法です。
SHAPは、モデルの予測を個々の特徴量に対してどれだけの貢献度があるかを評価し、解釈可能な形で提示することができる手法です。
今回はSHAPの基本的な考え方や実装方法について触れていきたいと思います。

機械学習モデルを解釈する指標SHAP

提案されている論文は以下になります。

指標そのものというよりも計算フレームワークに近いため、木構造系のモデルから深層学習モデルまでと様々な幅広いモデルに適用可能な方法です。

ゲーム理論の考え方から導出しているようで、特徴量をプレイヤーとみて、各プレイヤーが連携してゲームを進め、そのプレイヤーがどの程度ゲームに貢献したかという協力ゲーム理論に基づいた算出方法を利用しているようです。

各特徴量の予測への寄与度が\phi_iで、特徴量を使ったかどうかのバイナリベクトル空間上の関数で、説明したい関数fに近似します。
これを以下の３つの仮定の元で、各特徴量の寄与度\phi_iは一意に求まることが、ゲーム理論により示されているとのことです。

このSHAPは求めるのにかなりの計算量が必要なのですが、以下の論文では、木構造の仕組みをうまく使って、効率的にSHAPを求めるアルゴリズムを提案しています。

少し話が逸れますが、決定木やランダムフォレストなどの木構造アルゴリズムでは、特徴量の境界で切り分けた時のジニ係数を元にして、どの特徴量がより切り分けに効いているかをfeature_importanceで調べることができます。
しかしこの指標では、評価に一貫性が保たれない場合がある(Inconsistency)ことも述べられており、例えば、決定木のノードで使う特徴量を寄与度の高い特徴量に変更すると、その特徴量の寄与度が下がってしまうといった現象が起こります。

一方でSHAPを使うことによっこのfeature_importanceにおけるInconsistencyであることの問題は解消できると論文では言及されています。

加えて、相互作用効果を考慮したSHAP値(SHAPE Interaction Values)も提案されています。

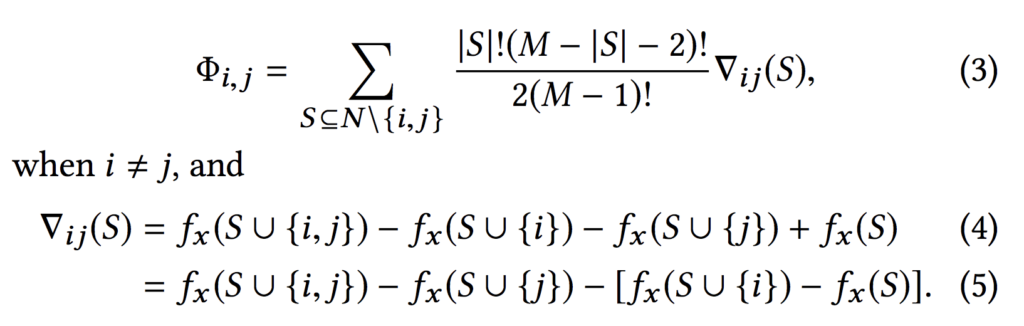
深くは読んでいないのですが、恐らくSHAPと同じ考え方で2つの特徴量を使った時の寄与度を求めることができ、これを1つだけの特徴量の寄与度から差っ引いて1つの特徴量の主効果を計算することができる、という話ではないかと思います。

何はともあれ、早速使ってみようと思います。
SHAPは様々な機械学習タスクに適用可能なので、回帰系タスク・分類系タスクについてそれぞれ見てみます。

回帰系モデルへの適用

SHAPは以下のライブラリから利用することができます。

Pythonの場合はラッパーが用意されているので、pip install shapでインストール可能です。

まずは回帰系モデルに対して使ってみます。
sklearnのボストン住宅価格の分析タスクをLightGBMで解いてみて、どの特徴量が効いているのかを、SHAPで確認してみます。

import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pylab as plt
from sklearn import datasets, model_selection, metrics
import lightgbm as lgb
import shap

# load JS visualization code to notebook
shap.initjs()

# 回帰系
boston = datasets.load_boston()
df_boston = pd.DataFrame(data=np.c_[boston['data'], boston['target']], columns=boston['feature_names'].tolist() + ['target'])
display(df_boston.head())

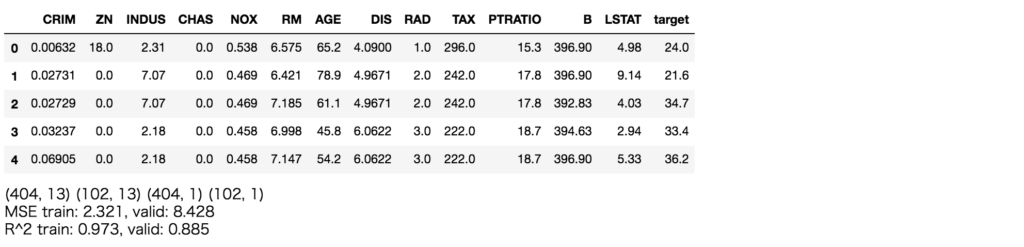
train_X, valid_X, train_y, valid_y = model_selection.train_test_split(df_boston[boston['feature_names'].tolist()], df_boston[['target']], test_size=0.2, random_state=42)
print(train_X.shape, valid_X.shape, train_y.shape, valid_y.shape)

model = lgb.LGBMRegressor()
model.fit(train_X, train_y)

print('MSE train: %.3f, valid: %.3f' % (
    metrics.mean_squared_error(train_y, model.predict(train_X)),
    metrics.mean_squared_error(valid_y, model.predict(valid_X))
))
print('R^2 train: %.3f, valid: %.3f' % (
    metrics.r2_score(train_y, model.predict(train_X)),
    metrics.r2_score(valid_y, model.predict(valid_X))
))

上記のshap.initjs()はJupyter notebookで実行する際に必要です。
恐らくSHAPの結果の可視化にJavascriptが使われているので、そのための設定と思われます。

さて、以下を実行して、学習したモデルを使ってSHAPを計算します。

explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(train_X)

例えばある一つのサンプルデータをモデルで予測させた時、どの特徴量を見ていたかについて、以下のforce_plotで確認することができます。

print(train_y.iloc[0,:])
display(shap.force_plot(explainer.expected_value, shap_values[0,:], train_X.iloc[0,:]))

入力されたサンプルの各特徴量の値と、それが予測に対して正の方向に働いたものを赤色、負の方向に働いたものを青色としてプロットされます。
例えばこのサンプルにおいては、LSTAT=24.91であり、この値は予測に対して負の方向に作用している見てとれます。

全てのサンプルデータについても、force_plotで以下のように一気に確認することができます。

shap.force_plot(explainer.expected_value, shap_values, train_X)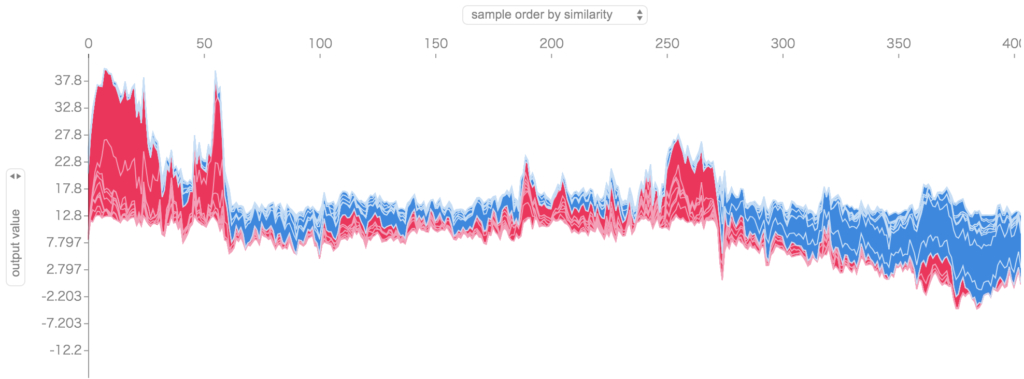

横軸にサンプルが並んでおり(404件)、縦軸にモデルの予測値、どの特徴量がプラス、マイナスに働いたかを確認できます。

一方で特徴量軸から見たい場合は、summary_plotで確認できます。

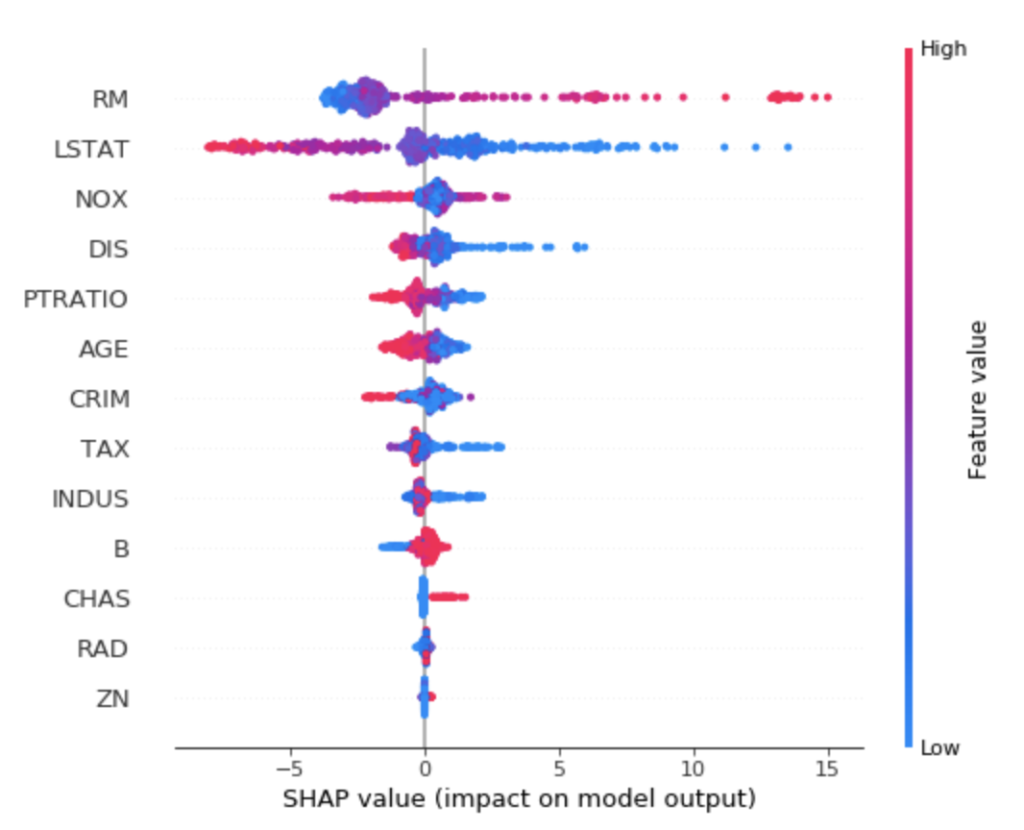
ドットが各サンプルデータで、横軸がSHAP値を表しており、色が特徴量の大小を表しています。
例えば、RMは高ければ予測値も高くなる傾向にあり、低ければ予測値も低くなる傾向があるようです。
LSTATは逆のようで、高ければ予測値は低くなり、低ければ予測値は高くなる傾向にあるようです。

以下のようオプションを指定すると、絶対値でSHAPの特徴量軸を比較してプロットでき、プラスマイナス含めて結局どの特徴量が予測に重要かが視覚化できます。

shap.summary_plot(shap_values, train_X, plot_type='bar')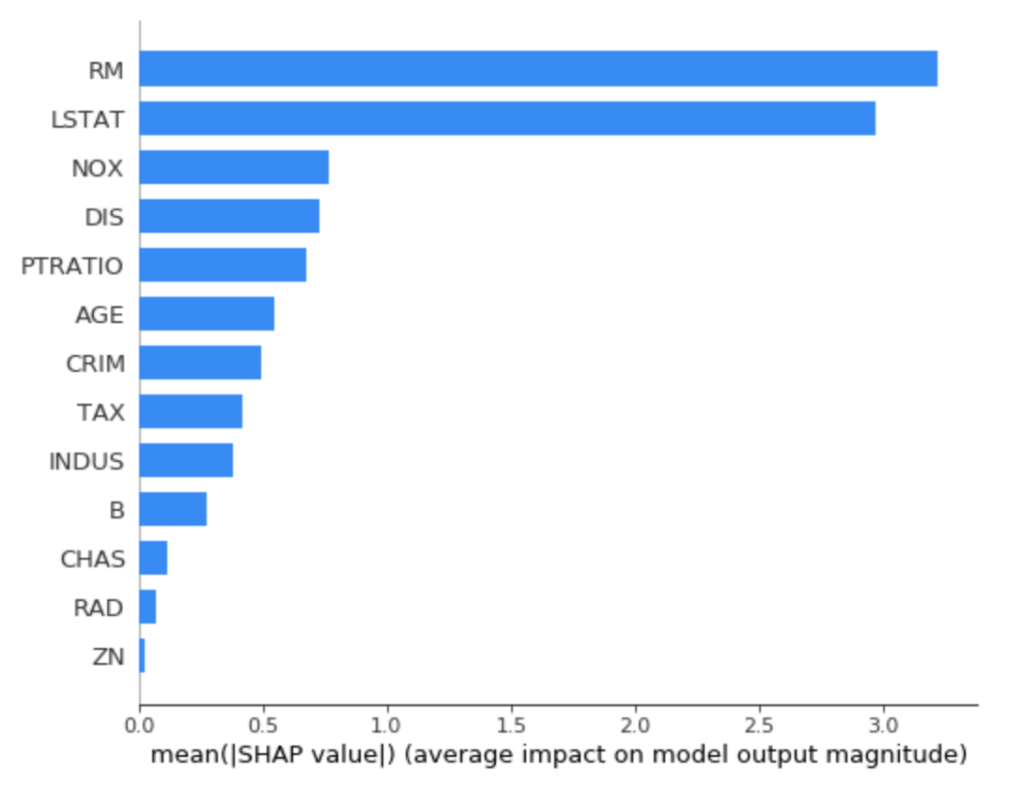

さらに、以下のようにして、ある特徴量だけに注目したグラフも可視化できます。

shap.dependence_plot('RM', shap_values, train_X, interaction_index='RM')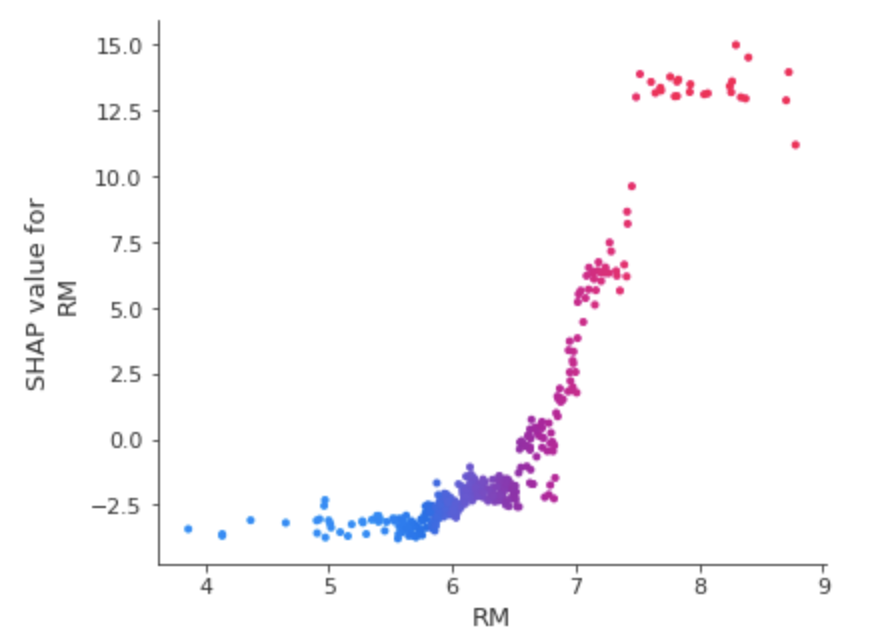

ドットがサンプルデータで、横軸が対象特徴量軸の値、縦軸が対象特徴量軸のSHAP値になります。
これを見ても、RMが高くなればなるほど、SHAP値も高くなる傾向にあり、予測値が上がることが分かります。
実際に学習データのRMとtargetの相関係数も0.71でした。
また、interaction_index引数で相互作用効果を見るための特徴量を選択できます。
何も指定しないと勝手に別の軸が選ばれて？きて、カラーバーがついて一瞬戸惑いますが、上記のように自分自身(同じ軸)を指定して、ただ1つの軸のみに注目させることもできます。

次に、Interaction SHAPを計算してみます。

shap_interaction_values = explainer.shap_interaction_values(train_X)

summary_plotで、各特徴量軸のペアについてのSHAPを確認することができます。

shap.summary_plot(shap_interaction_values, train_X)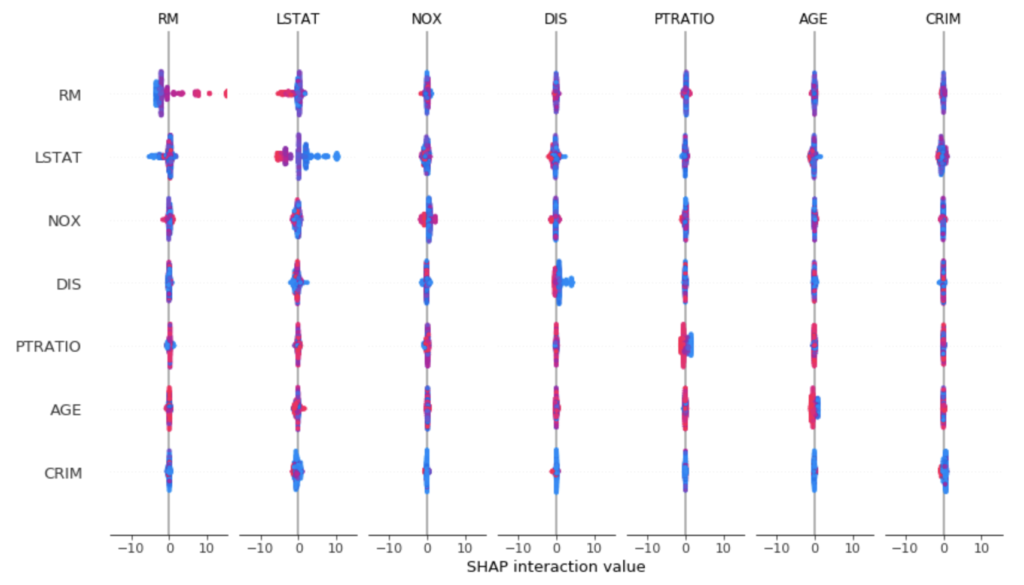

ある特徴量xと特徴量yの相互作用効果によるSHAPを見たい場合は、以下で確認できます。

shap.dependence_plot(('RM', 'LSTAT'), shap_interaction_values, train_X)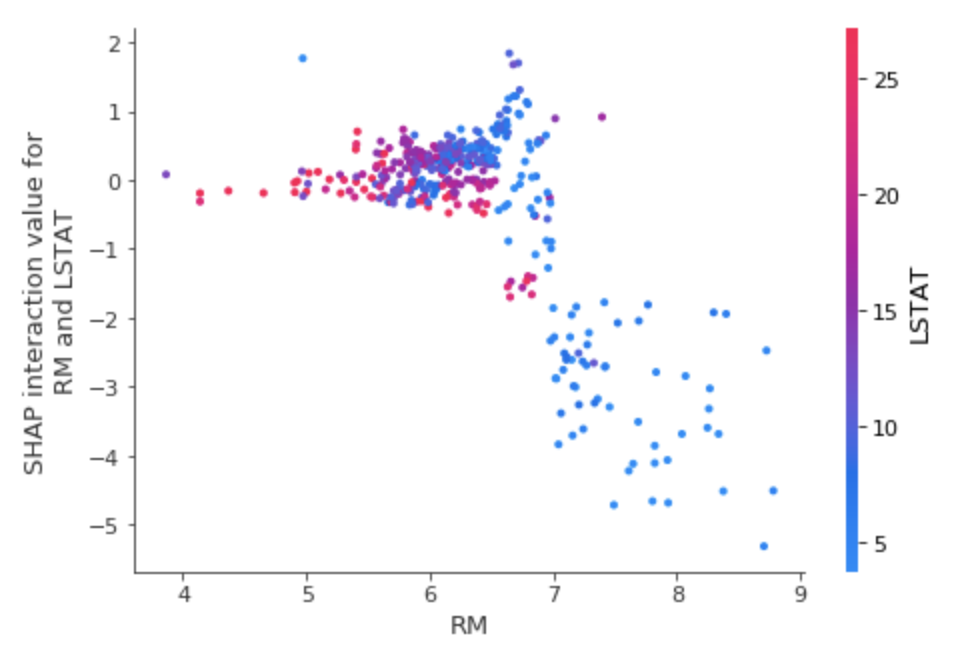

先ほどRM単体だけで見ると、高ければ高いほど、SHAPが高くなる傾向があったかと思いますが、ここでは逆転しています。
これはLSTATに引っ張られるということでしょうか。

shap.dependence_plot('LSTAT', shap_values, train_X, interaction_index='RM')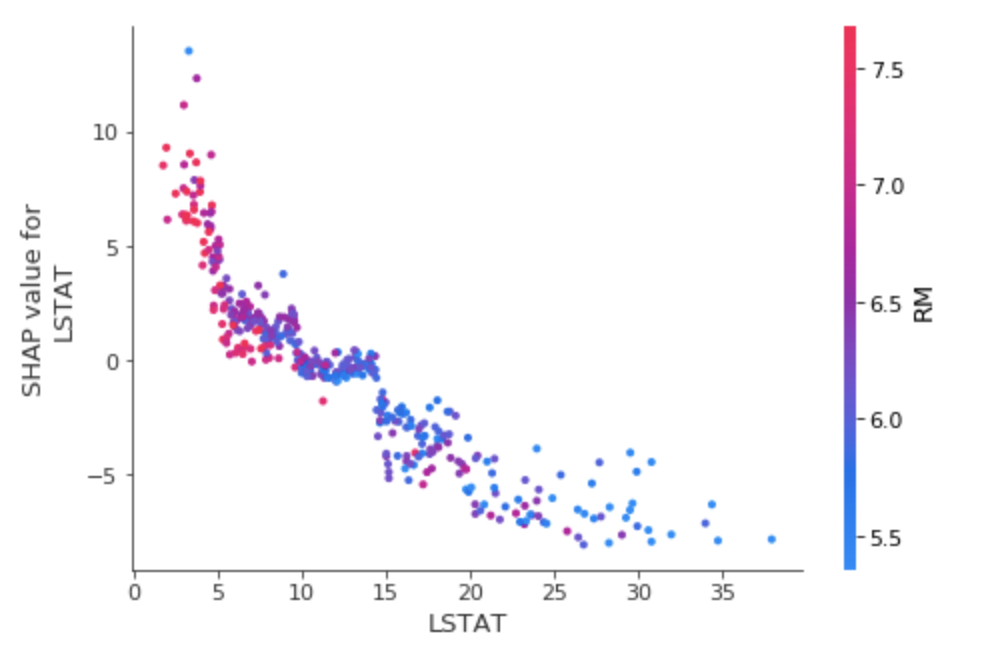

どうやらそういうことかもしれません。

ひとまず回帰系モデルでは以上のように、特徴量の大小が予測値に対してどう影響するかを確認できることが分かりました。

分類系モデルへの適用

分類系のモデルについても、同様にどの特徴量が効いているのかを可視化することができます。
同様に、sklearnのあやめの種類分類タスクをLightGBMで解いてみて、SHAPで確認します。

# 分類系
iris = datasets.load_iris()
df_iris = pd.DataFrame(data= np.c_[iris['data'], iris['target']], columns= iris['feature_names'] + ['target'])
display(df_iris.head())

train_X, valid_X, train_y, valid_y = model_selection.train_test_split(df_iris[iris['feature_names']], df_iris[['target']], test_size=0.2, random_state=42)
print(train_X.shape, valid_X.shape, train_y.shape, valid_y.shape)

model = lgb.LGBMClassifier()
model.fit(train_X, train_y)

print('Accuracy train: %.3f, valid: %.3f' % (
    metrics.accuracy_score(train_y, model.predict(train_X)),
    metrics.accuracy_score(valid_y, model.predict(valid_X))
))

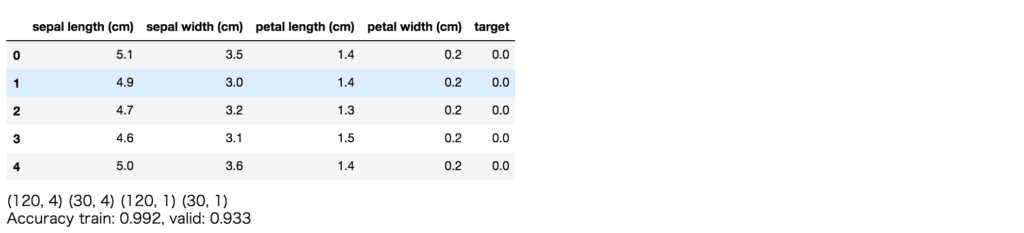
分類モデルに関しては、各クラスに対するSHAPを各特徴量について出力するようです。
あやめのデータは3クラス分類ですので、各クラスについて特徴量がどうだったから、そうであると予測した、そうでないと予測した、みたいな見方になります。

print(train_y.iloc[0,:])
print('')
for i in range(3):
    print('Class ', i)
    display(shap.force_plot(explainer.expected_value[i], shap_values[i][0,:], train_X.iloc[0,:]))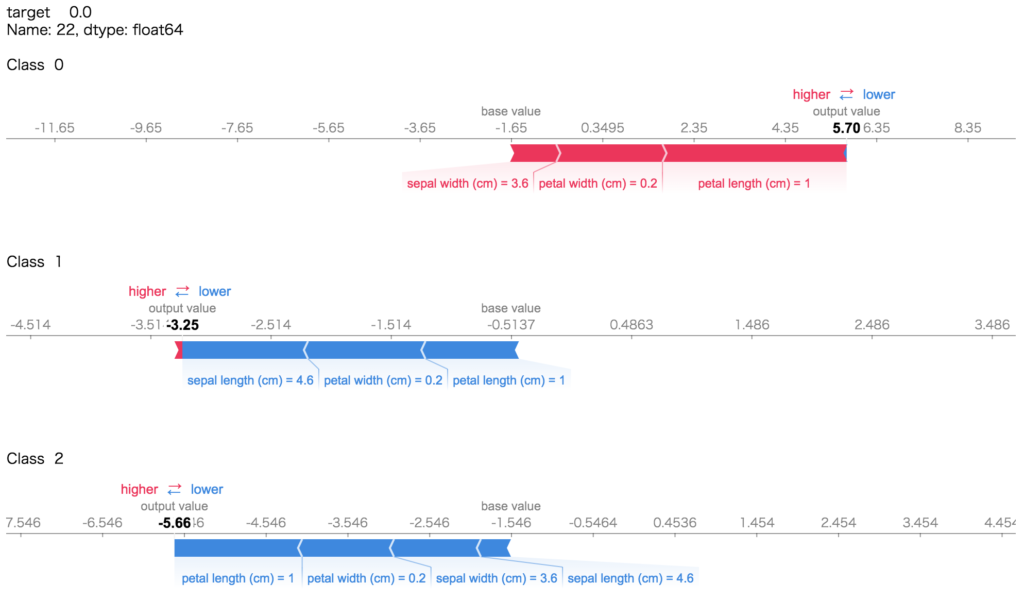

すべてのサンプルについても同様にして、

for i in range(3):
    print('Class ', i)
    display(shap.force_plot(explainer.expected_value[i], shap_values[i], train_X))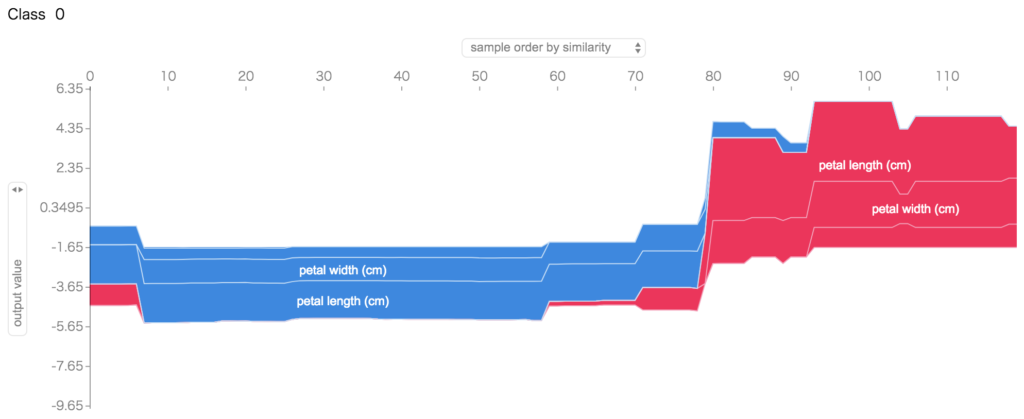

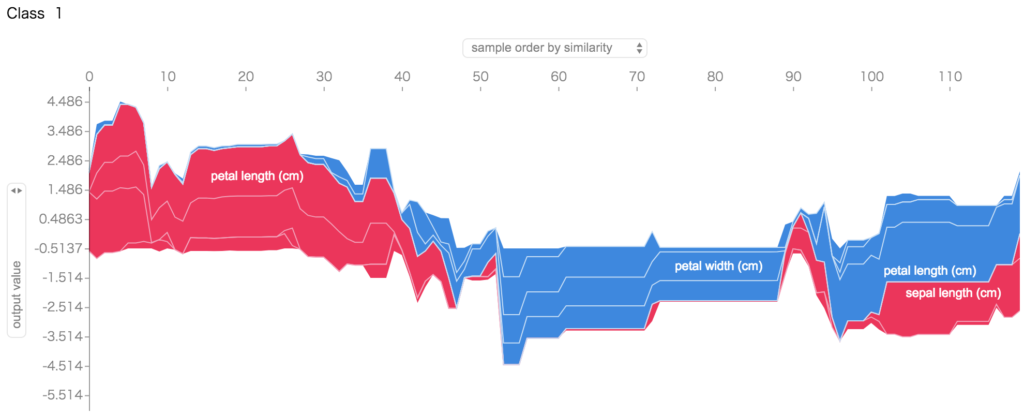
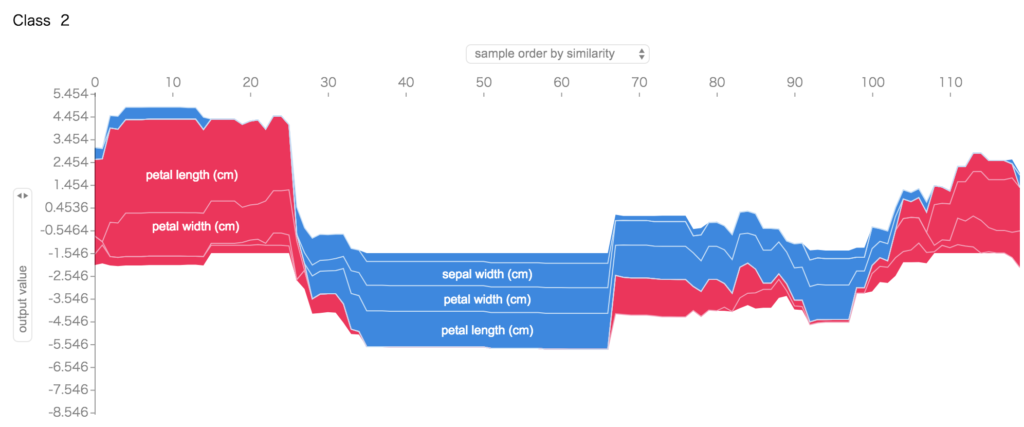
として、特徴量とそのクラスかそうでないかの判定の傾向が分かります。

summary_plotは以下のようにプロットされます。

shap.summary_plot(shap_values, train_X)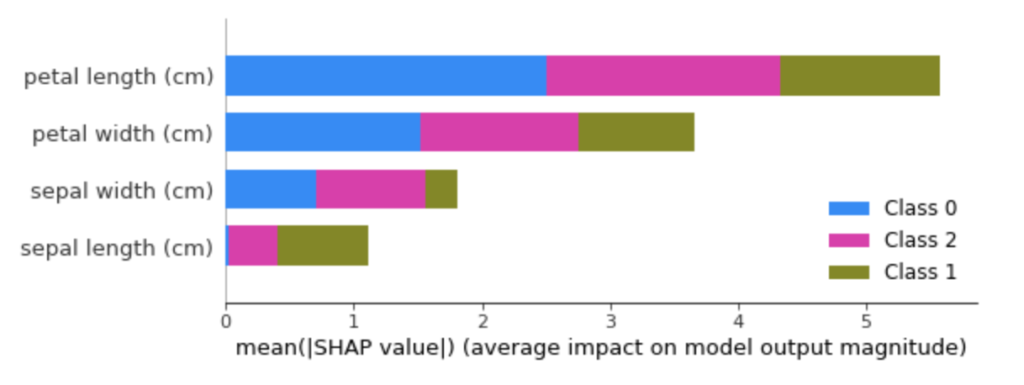

積立棒グラフで、それぞれの特徴量・クラスに対しての寄与度を可視化できます。
同様にして、他の指標も同じように確認できますので、以降は省略します。

深層学習モデルへの適用

深層学習モデルは手元では試しませんでしたが、公式ページによれば以下のように、深層学習モデルについても特徴量の寄与度の可視化が可能です。

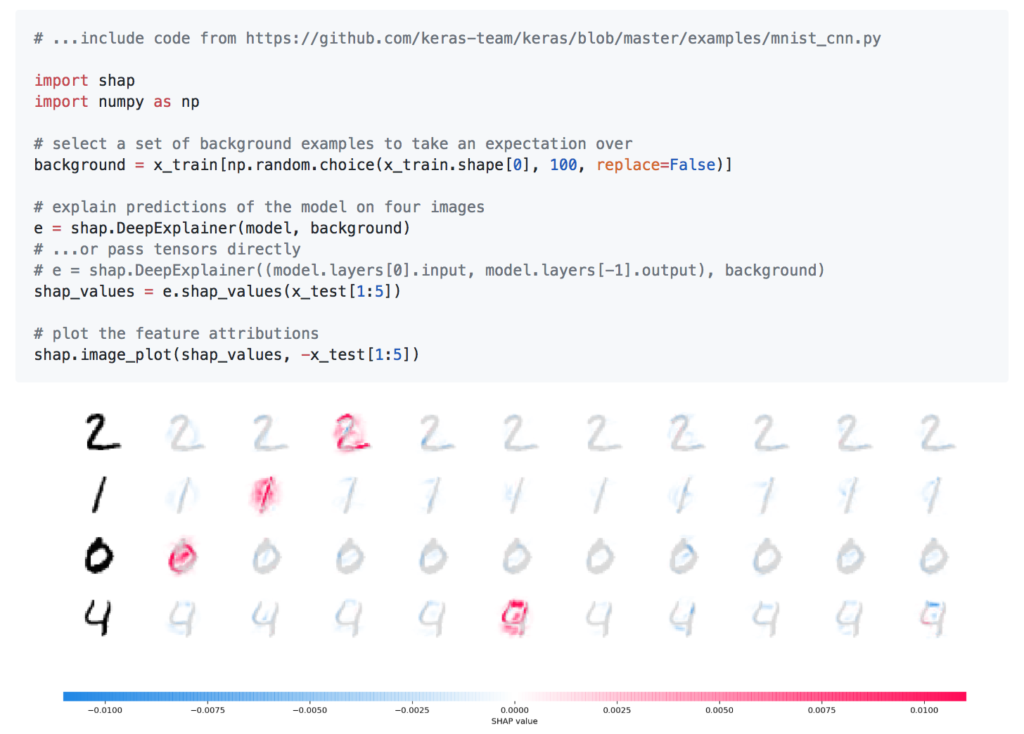
異なる考え方から導出されているGrad-CAMとの比較も試してみたいところです。
機会があればやってみようと思います。

まとめ

今回は機械学習モデルの解釈可能性に焦点を当て、その解釈手法の一つであるSHAPについて紹介しました。

仕事で機械学習モデルを学習させた時には、どういった理由でこのような予測しているのかといったロジックを要求されることが多々あります。
これまでご紹介した通り、SHAPは、特徴量ごとにモデルの予測に対する貢献度を評価し、その結果を解釈可能な形で提示する手法です。
この手法の導入により、モデルの予測結果がなぜそうなったのかを理解し、どの特徴量が重要であるかを把握することができます。

また、SHAPはモデルの種類を問わない統一フレームワークなので、複数の異なるモデルを、解釈を元に比較検討する際にも有効な手段と言えるでしょう。

スポンサーリンク