Kaggleデータセットを眺めていたとき、プロテニスの各プレイヤー各試合ごとのファースト・セカンドサービスでの取得ポイントや、リターン時取得できたポイントなど、詳細な結果が記録されているデータセットを見つけました。
テニス選手のプレーを定量化し理解することは容易ではありません。
例えば、各プレイヤーにはサーブが得意な選手やリターンが得意な選手がいると思いますが、果たしてそれは数値的にどのくらい強いのでしょうか。(戦闘力?)
そこで今回は、プロテニスの試合結果から得られた詳細なデータを活用し、各プレイヤーにはサーブ力とリターン力の潜在変数があると仮定して、因子分析で推定し定量化する試みをご紹介します。
因子分析は、多変量データから潜在的な因子を抽出する統計的手法であり、テニスの場面に応用することで、選手の特徴をより客観的に評価する手段になります。
分析の準備
今回使ったデータセットは下記になります。
テーブルはいくつか格納されていますが、使ったテーブルはall_matches.csvです。
各テニスプレイヤーのATPツアー試合結果が詳細なポイントまで含めてデータ化されており、2018年の試合分まで格納されています。
多くのカラムが入っていますが、今回の分析ではファースト・セカンドサービスやリターンのポイントに関する以下のカラムを利用することにします。
| カラム名 | カラムの意味 |
|---|---|
| player_name | プレイヤー名 |
| player_victory | 勝敗 |
| double_faults | ダブルフォルト数 |
| first_serve_made | ファーストサービスが入った数=first_serve_points_attempted |
| first_serve_attempted | ファーストサービスをおこなった数 |
| first_serve_points_made | ファーストサービス成功時の獲得ポイント数 |
| first_serve_points_attempted | ファーストサービス成功時の全体ポイント数=first_serve_made |
| second_serve_points_made | セカンドサービス成功時の獲得ポイント数 |
| second_serve_points_attempted | セカンドサービス成功時の全体ポイント数 |
| first_serve_return_points_made | 相手ファーストサービス成功時(リターン)の獲得ポイント数 |
| first_serve_return_points_attempted | 相手ファーストサービス成功時(リターン)の全体ポイント数 |
| second_serve_return_points_made | 相手セカンドサービス成功時(リターン)の獲得ポイント数 |
| second_serve_return_points_attempted | 相手セカンドサービス成功時(リターン)の全体ポイント数 |
| doubles | ダブルスかどうか |
| masters | トーナメントのATPポイント(例:2000=グランドスラム) |
データをPandasで読込んで分析の準備をします。
直近の試合分のデータで分析したいので、2016年以降のデータに限定し、シングルスのみを取得しました。
データには、各プレイヤーが各試合ごとにファースト・セカンドサービスを何回実施し、何回成功したか、ポイントがいくつ取れたかなどが入っています。
各試合で実施された合計ポイント数は試合によって異なりますので、その試合中での成功率やポイント率などの割合に変換します。
また、チャレンジャーなど下位の試合のデータも含まれており、分析対象が多すぎますので、今回は2016年以降に開催されたグランドスラムに出場したことがあり、かつ10回以上の白星をあげているプレイヤーに絞りました。
df_tmp = df_matches[df_matches['masters'] == 2000]
# ファーストサービス成功率
df_tmp.loc[:, 'first_serve_rate'] = df_tmp['first_serve_made']/df_tmp['first_serve_attempted']
# ファーストサービス成功時のポイント率
df_tmp.loc[:, 'first_serve_point_rate'] = df_tmp['first_serve_points_made']/df_tmp['first_serve_points_attempted']
# セカンドサービス成功率
df_tmp.loc[:, 'second_serve_rate'] = 1-df_tmp['double_faults']/df_tmp['second_serve_points_attempted']
# セカンドサービス成功時のポイント率
df_tmp.loc[:, 'second_serve_point_rate'] = df_tmp['second_serve_points_made']/df_tmp['second_serve_points_attempted']
# 相手ファーストサービス成功時のポイント率
df_tmp.loc[:, 'first_serve_return_point_rate'] = df_tmp['first_serve_return_points_made']/df_tmp['first_serve_return_points_attempted']
# 相手セカンドサービス成功時のポイント率
df_tmp.loc[:, 'second_serve_return_point_rate'] = df_tmp['second_serve_return_points_made']/df_tmp['second_serve_return_points_attempted']
# 勝敗
df_tmp.loc[df_tmp['player_victory'] == 't', 'victory'] = 1
df_tmp.loc[df_tmp['player_victory'] == 'f', 'victory'] = 0
get_cols = [
'player_name', 'first_serve_rate', 'first_serve_point_rate','second_serve_rate', 'second_serve_point_rate',
'first_serve_return_point_rate', 'second_serve_return_point_rate', 'victory'
]
df_tmp = df_tmp[get_cols]
df_tmp = df_tmp.groupby('player_name').agg(['mean','count'])
df_tmp = df_tmp[(df_tmp['victory']['count'] >= 10) & (df_tmp['victory']['mean'] > 0)]
levels = df_tmp.columns.levels
labels = df_tmp.columns.labels
df_tmp.columns = [levels[0][i]+'_'+levels[1][j] for i, j in zip(labels[0], labels[1])]
df_tmp = df_tmp[[c+'_mean' for c in get_cols[1:]]]
df_tmp.columns = get_cols[1:]
df_tmp_n = (df_tmp-df_tmp.mean())/df_tmp.std()
df_tmp_n = df_tmp_n.dropna()
len(df_tmp_n) # 81まずは各カラムで相関をとってみて、上記であげた因子が仮定できそうか確認してみます。
plt.figure(figsize=(6,5))
sns.heatmap(df_tmp.corr(), annot=True, vmax=1, vmin=-1, fmt='.2f', cmap=cm)
plt.show()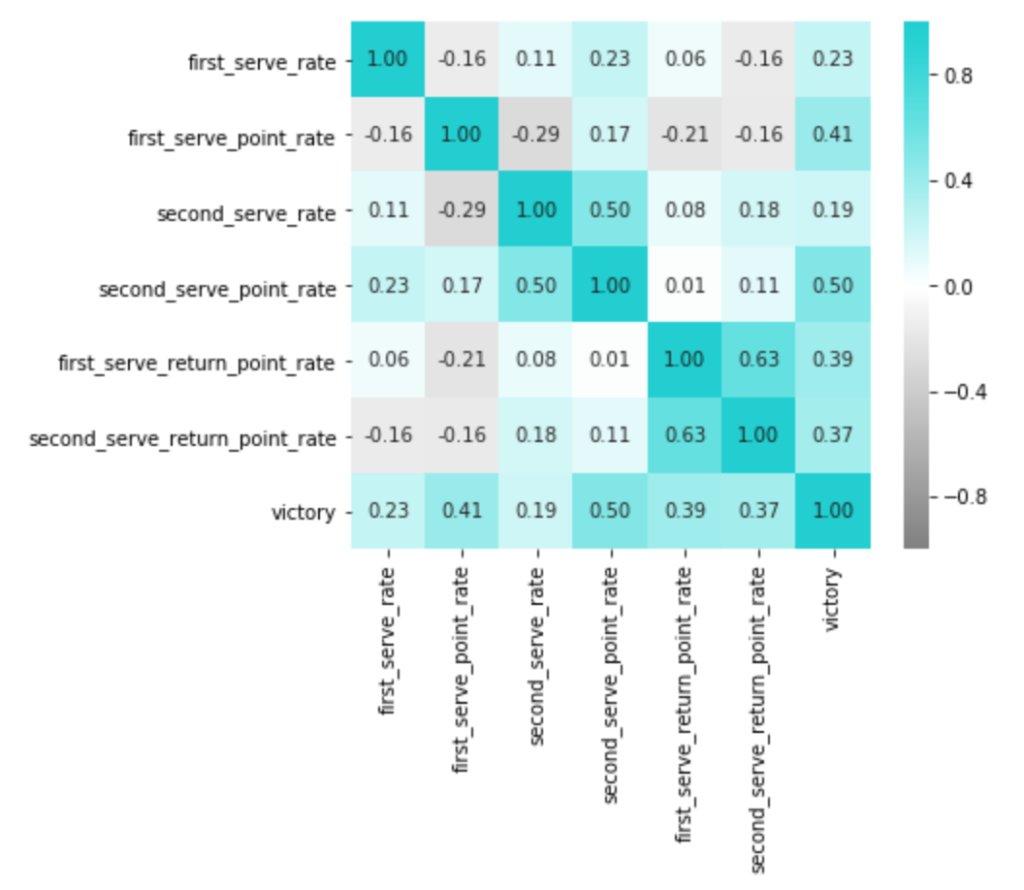
これを見る限り、ファースト、セカンド両方とも、サーブの成功率(精度)とポイント率はあまり相関しないようです。
言われてみれば当たり前ですが、精度とポイント率でみれば、勝敗に対してより相関があるのはポイント率の方。
このクラスになると、もうサーブの精度なんてものは一定以上あって、その後のゲームメイクの方がより重要になるようです。
またこれも意外な面白いところですが、ファーストサービスからのポイント率とセカンドサービスからのポイント率はあまり相関していないようです。
サービスのゲーム展開が得意な選手の中でも、それがファーストの場合は得意であっても、セカンドの場合は得意とは限らないみたいです。
逆にリターンに関しては予想通りで、リターンが得意な選手は相手がファーストでもセカンドでも強い傾向があるようです。
この結果、サーブ力・リターン力の2つの因子と仮定するよりも、ファーストサービス(のゲームメイク)力・セカンドサービス(のゲームメイク)力・リターン力の3つの因子が潜在していると解釈できそうな気がしてきました。
実際に分析してみないと分からないので、因子数を2〜4で設定して、各結果について、因子負荷量と各選手の因子得点の様子を確認してみます。
因子の数を指定して、分析結果を返却する関数、分析結果から因子得点の散布図をプロットする関数を以下のように作成しました。
x = df_tmp_n[target_cols].values
y = df_tmp_n.index
def fit(factor_num):
fa = decomposition.FactorAnalysis(n_components=factor_num).fit(x)
df_factor_loading = pd.DataFrame(columns=target_cols)
for i in range(factor_num):
df_factor_loading = df_factor_loading.append(pd.Series(fa.components_[i], index=target_cols, name='factor'+str(i)))
display(df_factor_loading)
return fa
def plot(factor_num, fa):
transformed = fa.fit_transform(x)
for i, j in itertools.combinations(np.arange(factor_num), 2):
plt.figure(figsize=(8,8))
plt.scatter(transformed[:, i], transformed[:, j], color=base_color)
for k, y_ in enumerate(y):
plt.annotate(y_, xy=(transformed[k, i], transformed[k, j]), size=8, alpha=0.5)
fai = fa.components_[i]
faj = fa.components_[j]
for k, c in enumerate(target_cols):
plt.arrow(0, 0, fai[k]*2, faj[k]*2, color='r', head_width=0.1, alpha=1)
plt.text(fai[k]*2.5, faj[k]*2.5, c, color='r', fontsize=12)
plt.axes().add_patch(plt.Circle((0, 0), radius=0.5*2, ec='r', fill=False))
plt.xlim([-3,3])
plt.ylim([-3,3])
plt.xlabel('factor'+str(i))
plt.ylabel('factor'+str(j))
plt.title('factor'+str(i)+' x '+'factor'+str(j))
plt.show()
return transformed因子数2と仮定した時の分析結果と解釈
まずは因子数2の場合で、因子負荷量を確認してみます。
fa2 = fit(factor_num=2)
transformed2 = plot(factor_num=2, fa=fa2)
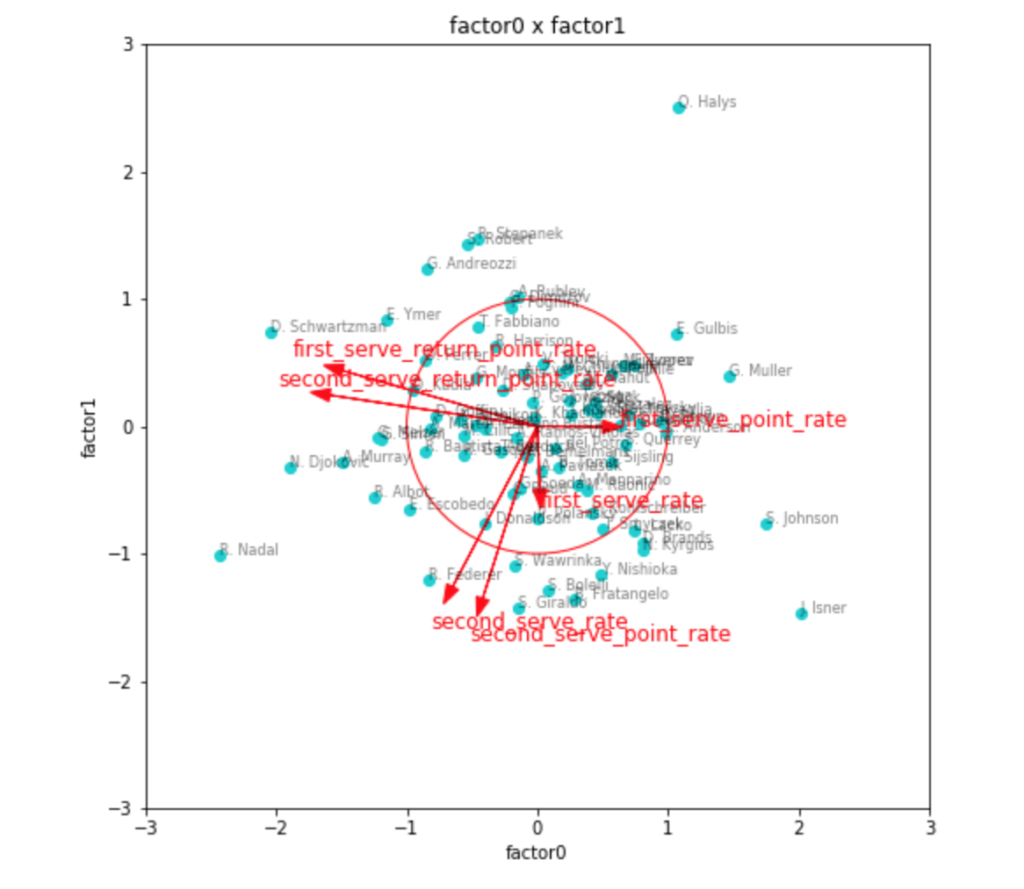
因子得点のプロットには、因子負荷量のベクトルと目安の0.5の円を同時に描いてみました。
やはりこれで見ると、リターン力に関しては1つの因子として取れそうですが、サーブに関する情報がうまくまとまらなそうです。
強いて言えば、リターン力・セカンドサービス力の2つの因子が潜在するということにはなりそうですが、因子負荷量としてはもう少し大きく出てほしいところ。
因子数3と仮定した時の分析結果と解釈
次に因子数3の場合を見てみます。
fa3 = fit(factor_num=3)
transformed3 = plot(factor_num=3, fa=fa3)
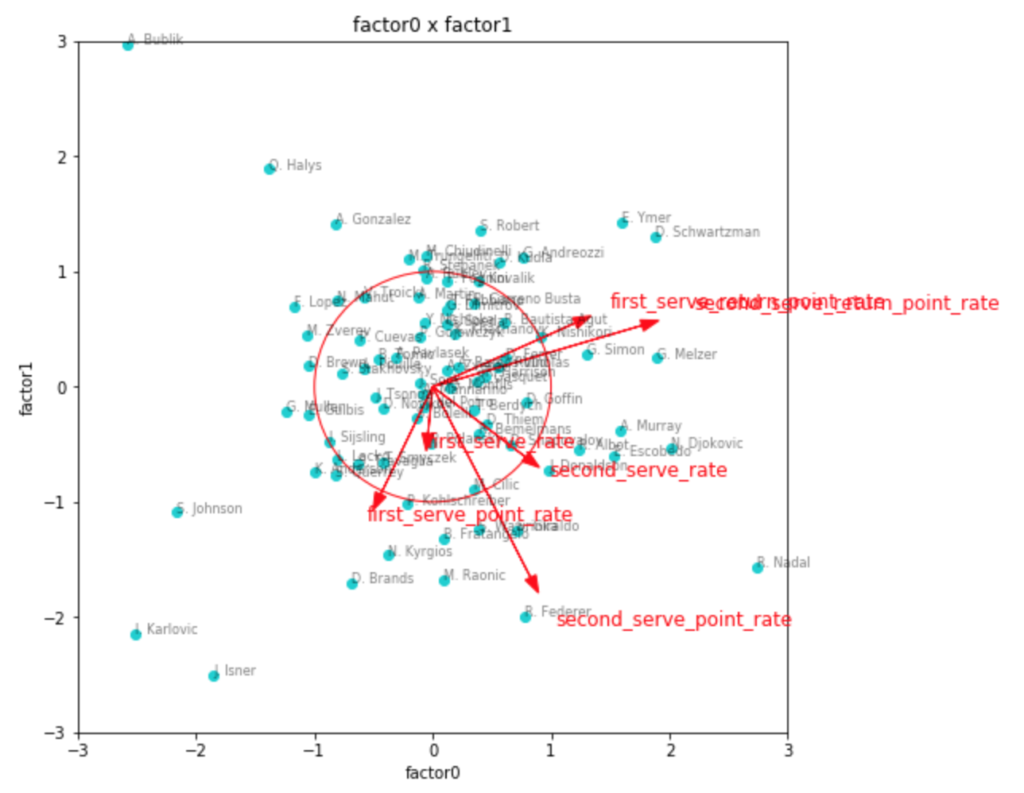
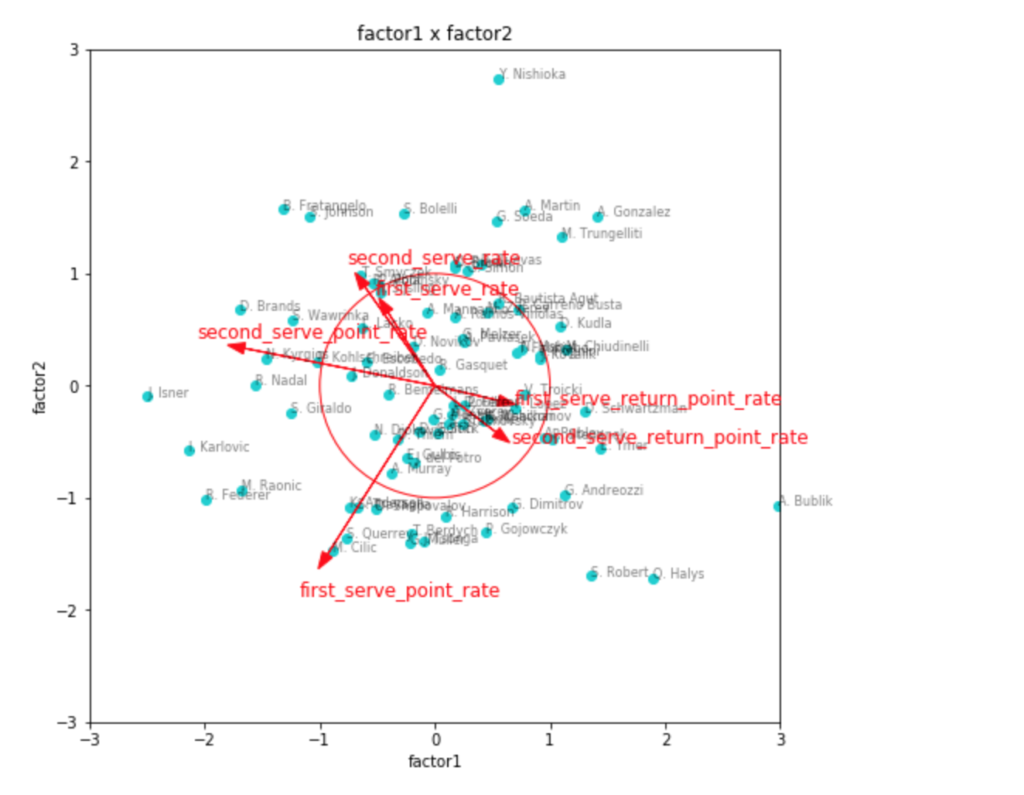
因子負荷量を見ても、やはりこれが一番しっくりきそうな感じです。
第1因子がリターン力、第2因子がセカンドサービスでのポイント力、第3因子がファーストサービスでのポイント力といったところでしょうか。
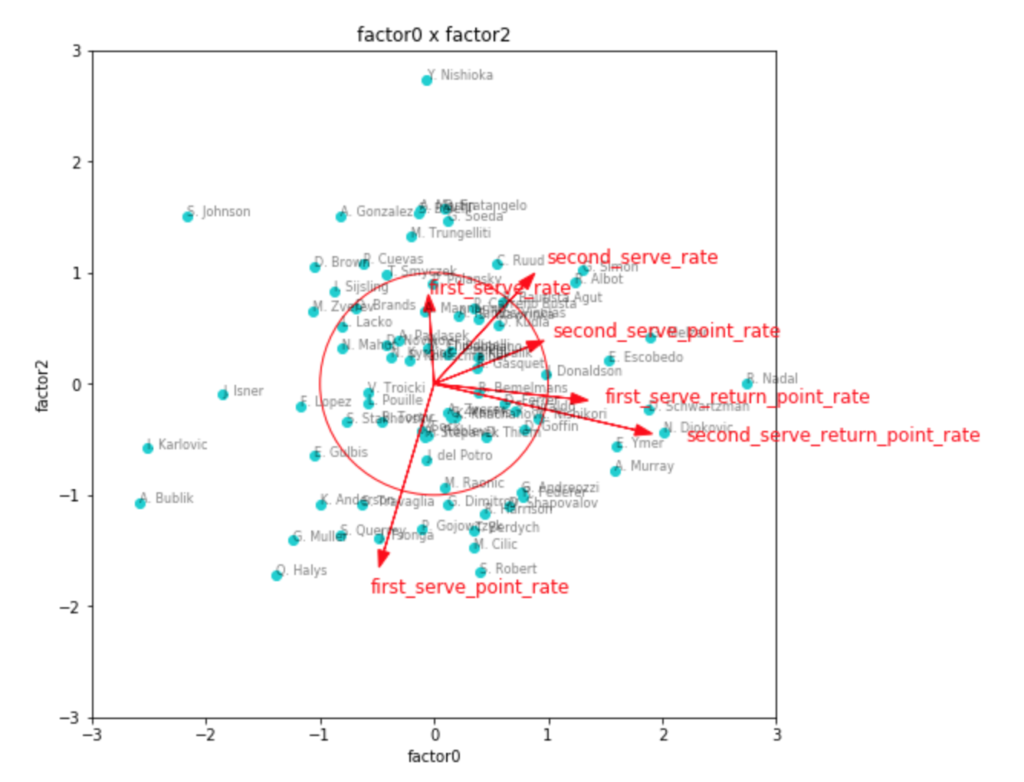
因子得点の3つ目のグラフを見てみると、見事に左下にビッグサーバー選手が集まっていて面白いです。
ファーストサービス方向にチリッチやクエリー、アンダーソンなどの選手がいて、かつセカンドサービス方向にも強いと位置しているのが、フェデラーやラオニッチ、カルロビッチといった選手で、サービスが武器と言われている選手の中でも、勝率としてより成功している選手は、両方の軸で強い位置に出てきているように見えます。
リターン力で見ると、ナダルやジョコビッチ、シュワルツマンなどが強いようです。
ちょっと重なって見えづらいですが、錦織選手もリターン力が強い位置にいます。
因子数4と仮定した時の分析結果と解釈
最後に因子数4の場合もやってみます。
fa4 = fit(factor_num=4)
これはやはり予想通りで、なんだかよくわからない結果になってしまいました。
因子負荷量の絶対値がどれもそこそこの大きさになってしまって、どの因子が何を表しているのかはっきりしません。
これについては因子得点のプロットは省略します。
まとめとおまけ
以上、今回のデータからは、因子はファーストサービス(のゲームメイク)力・セカンドサービス(のゲームメイク)力・リターン力の3つから生成されると解釈した方が良さそうです。
以下のように、各因子と勝率の相関を見てみると、
df_results = pd.DataFrame(
np.concatenate([np.array(y).reshape(len(y), 1), transformed3, df_tmp['victory'].values.reshape(len(y), 1)], axis=1),
columns = ['player_name', 'factor0', 'factor1', 'factor2', 'victory_rate']
)
df_results['factor0'] = df_results['factor0'].astype(np.float32)
df_results['factor1'] = -df_results['factor1'].astype(np.float32)
df_results['factor2'] = -df_results['factor2'].astype(np.float32)
df_results['victory_rate'] = df_results['victory_rate'].astype(np.float32)
plt.figure(figsize=(6,5))
sns.heatmap(df_results.corr(), annot=True, vmax=1, vmin=-1, fmt='.2f', cmap=cm)
plt.show()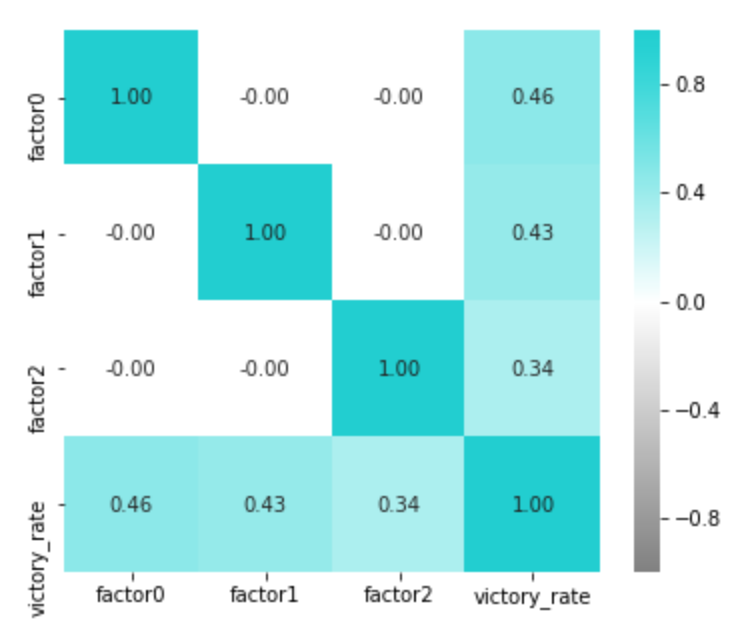
当たり前ですが、どれも大事そうです。
強いて言うならば、勝つためにはやはりリターンでよりゲーム数をもぎ取る必要があるので、リターン力の因子がより勝率との相関が強めに出ています。
最後に、これらの各因子の得点で定量的に見た錦織選手の順位を調べてみると
print('K. Nishikori')
print('-'*50)
for i in [0, 1, 2]:
rank = np.where(df_results.sort_values(by='factor'+str(i), ascending=False)['player_name'].values == 'K. Nishikori')
rank = rank[0][0]+1
print('factor'+str(i), '\t', rank, '/', len(df_results))K.Nishikori
--------------------------------------------------
factor0 11/81
factor1 54/81
factor2 31/81となりました。
リターン力はかなり上位の位置にいます。
一方で、セカンドサーブがあまり強くなくやられてしまう傾向はあるみたいで、これは実際の試合などを見ていても納得できる結果となりました。
いかがだったでしょうか?
今回はプロテニスの試合結果から得られた詳細なデータを元に、因子分析を用いてサーブ力とリターン力を定量化するアプローチを取り上げました。
因子分析により、テニス選手の要素的な強さを客観的かつ網羅的に評価することが可能となりました。最後に錦織選手の例を見せたように、サーブ力やリターン力といったふわっとしているが重要な要素を数値化してランキング化し、選手の強みや改善すべき点をより明確に把握することができます。
皆さんもぜひ興味のある身近な例で試してみて、質的な洞察を得てみてください。
