状態空間モデルは、時系列データや観測データの背後にある潜在的な状態を推定するための強力な統計的手法です。
本記事では、状態空間モデルの基本的な概念と、Statsmodels、PyStan、PyMC、Edwardといった各種Pythonライブラリを使用した簡単なコーディング例を紹介しようと思います。
状態空間モデルについて
状態空間モデルは、時系列データの解析に用いられる統計モデルの一つです。
時系列データは、時間に沿って観測されるデータの系列であり、例えば、毎日の気温、株価の変動、経済指標の変化などが該当します。
状態空間モデル自体は幅広い概念であり、元々は制御工学で開発された理論でした。
1970年代頃から、統計応用にも適用されるようになり、その後、金融データへの応用、例えば、ボラティリティの推定、債券価格やコモディティ価格のモデリングなどで、モデルの研究が進みました。
状態空間モデルは、以下の主要な要素から成り立っています:
- 状態方程式(State Equation): 状態方程式は、システムの内部の状態を表す差分方程式です。現在の状態を過去の状態と外部からの影響(制御入力)から予測する役割を果たします。制御工学の文脈では、この部分をシステム方程式と呼ぶこともあります。
- 観測方程式(Observation Equation): 観測方程式は、状態と直接関連づけられた観測値(観測データ)を表します。一般的に、時系列データの中で直接観測できる部分を示すために使用されます。
- 制御入力(Control Input)(オプション): 一部の状態空間モデルでは、外部からの制御入力が存在します。これは、状態に影響を与える外部要因を表すために使われます。
状態空間モデルは、観測されるデータと未観測の状態を同時にモデル化するため、時系列データの予測や推定に非常に有用です。
また、潜在的な状態を捉えることで、ノイズの除去やトレンドの特定など、より詳細な解析を行うことができます。
時系列分析のモデルとして広く知られるAR(自己回帰)モデル、MA(移動平均)モデル、ARMA(自己回帰移動平均)モデル、ARIMA(非季節性自己回帰移動平均)モデルなどは、状態空間モデルの特別なケースとして捉えることができます。
状態空間モデルはこれらのモデルの拡張として理解することができ、幅広い時系列データに対して適用可能な汎用性の高いモデルになっています。
近年では、状態空間モデルの応用範囲が広がり、金融データのモデリングからマーケティング分野における広告の影響の解析まで、様々な分野で活用されています。
今回は実装について記しますので、詳細は書籍などを参照すると良い思います。
時系列モデルに関する書籍も数多く出版されており、最近では下記などがおすすめです。
今回は状態空間モデルの中でも最も基礎となるローカルレベルモデルを各種ライブラリを使って実装してみる例をご紹介します。
Statsmodelsによる状態空間モデルの実装
まずはStatsmodelsによる状態空間モデルから見ていきます。
今回は以下のように適当な時系列データを作成し、これについてモデルを適用してみることにします。
import numpy as np
import matplotlib
import matplotlib.pylab as plt
%matplotlib inline
from tqdm import tqdm
y = np.cumsum(np.random.normal(size=100))
plt.plot(y)
plt.show()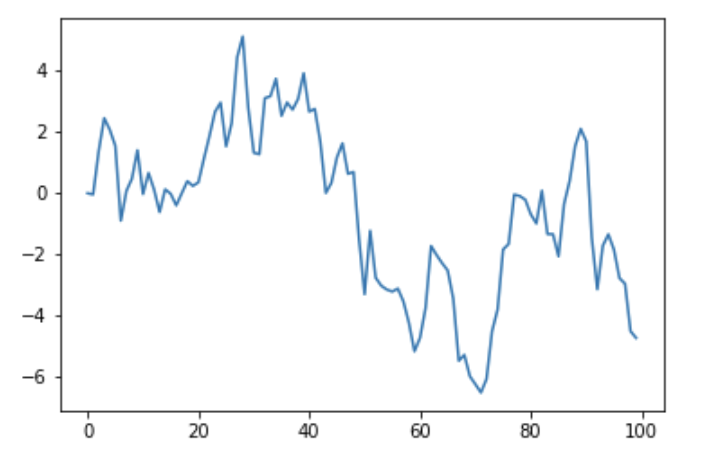
他のライブラリであれば、
モデルを実装 → パラメータを推定 → 結果を確認
と段階を踏んで実装するのが普通ですが、Statsmodelsでは、一連の流れをUnobservedComponents関数で全て一気にやってくれます。
import statsmodels.api as sm
model = sm.tsa.UnobservedComponents(y, 'local level')
result = model.fit()
result.plot_components()
plt.show()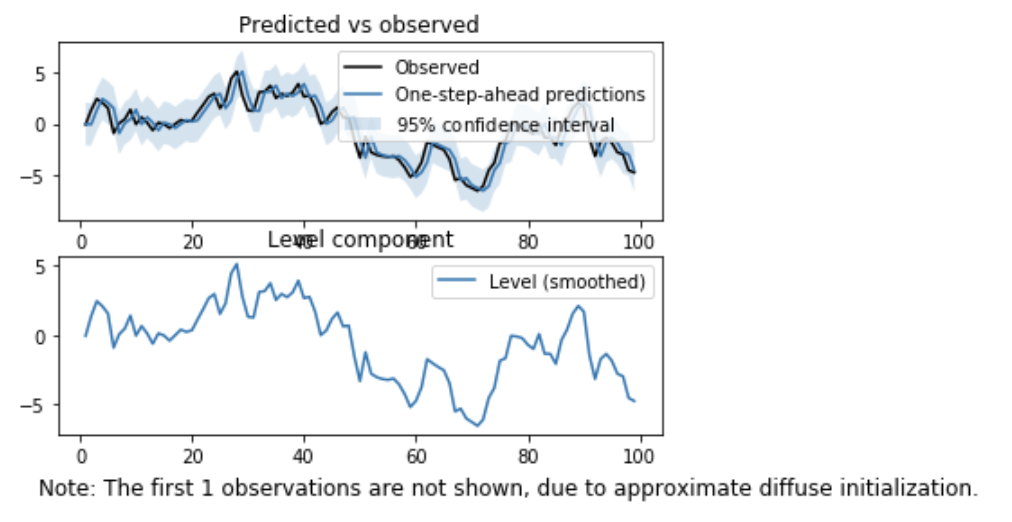
ローカルレベルでの推定は、引数に'local level'を指定します。
ライブラリ公式のページのうち、以下ページなどで詳しく解説されています。
PyStanによる状態空間モデルの実装
続いて、PyStanの場合の実装について見てみます。
前述の通り、PyStanの場合はStanでモデルを構築する必要があります。
別の言語の記法を覚えなければいけないのは面倒かもしれませんが、StanはRから実行できるラッパーのRStanもあり、どちらもモデル部分は同じStanで書きますので、ネット上で参考になる例が多く見つかります。
ローカルレベルモデルをモデル式で書くと、以下のようになります。
\(y_t=\mu_t+\epsilon_v,\epsilon_v{\sim}N(0,\sigma_v)\)
\(\mu_t=\mu_{t-1}+\epsilon_w,\epsilon_w{\sim}N(0,\sigma_w)\)
PyStanはこれをStanで記述した文字列を受け取ってPythonから実行します。
モデルの構築・学習のコードは以下の通り。
import pystan
model = """
data {
int n; # サンプルサイズ
vector[n] y; # 時系列の値
}
parameters {
real muZero; # 左端
vector[n] mu; # 確率的レベル
real sigmaV; # 観測誤差の大きさ
real sigmaW; # 過程誤差の大きさ
}
model {
# 状態方程式
mu[1] ~ normal(muZero, sqrt(sigmaW));
for(i in 2:n) {
mu[i] ~ normal(mu[i-1], sqrt(sigmaW));
}
# 観測方程式
for(i in 1:n) {
y[i] ~ normal(mu[i], sqrt(sigmaV));
}
}
"""
fit = pystan.stan(model_code=model, data={'n': 100, 'y': y}, iter=1000, chains=1)
fitInference for Stan model: anon_model_4eca5dff070c8e9e2e8fbdc5e7560772.
1 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero -0.02 0.05 1.07 -2.16 -0.74 -0.03 0.72 1.99 500 1.0
mu[0] -0.04 0.01 0.23 -0.48 -0.15 -0.03 0.07 0.46 500 1.0
mu[1] -0.01 9.9e-3 0.22 -0.42 -0.15 -0.04 0.1 0.54 500 1.0
mu[2] 1.32 8.5e-3 0.19 0.89 1.21 1.34 1.44 1.71 500 1.0
mu[3] 2.36 0.01 0.23 1.85 2.25 2.38 2.48 2.82 500 1.0
mu[4] 2.04 9.3e-3 0.21 1.61 1.93 2.04 2.16 2.45 500 1.0
mu[5] 1.44 0.01 0.24 0.9 1.32 1.46 1.57 1.9 500 1.01
mu[6] -0.78 0.05 0.23 -1.13 -0.93 -0.82 -0.66 -0.24 22 1.03
mu[7] 0.03 9.7e-3 0.22 -0.41 -0.09 0.03 0.14 0.5 500 1.0
mu[8] 0.46 0.01 0.23 -0.01 0.34 0.46 0.59 0.93 500 1.0
mu[9] 1.28 9.8e-3 0.22 0.75 1.18 1.31 1.41 1.68 500 1.0今回は簡単のために実装しましたが、ちゃんとやるならば本来はchainsを3以上に指定して、Rhatで収束しているか確認するべきかと思います。
一応上記はチェイン数1ですが、Rhatは収束していそうです。
上記のようにfitを出力すると結果は文字列で表示されますが、Pythonで推定したパラメータを配列で取得したい場合は以下のようにextract関数を使います。
la = fit.extract()
pred = la['mu'].mean(axis=0)
mu_lower, mu_upper = np.percentile(la['mu'], q=[2.5, 97.5], axis=0)
plt.plot(list(range(len(y)+1)), list(y)+[None], color='black')
plt.plot(list(range(1, len(y)+1)), pred)
plt.fill_between(list(range(1, len(y)+1)), mu_lower, mu_upper, alpha=0.3)
plt.show()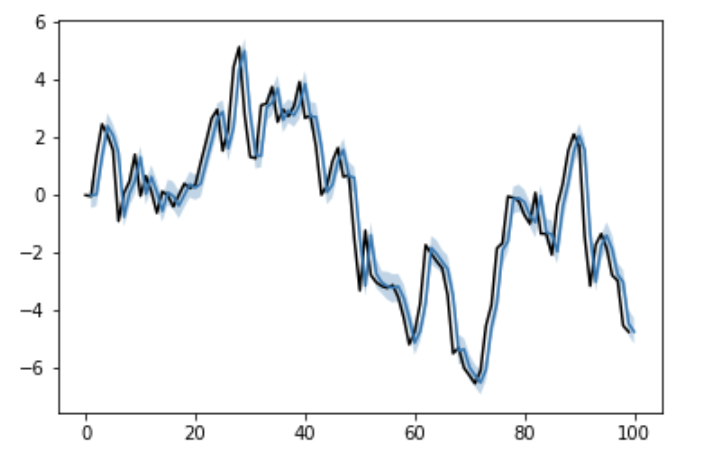
PyMC3による状態空間モデルの実装
PyMC3の場合も同様に、モデルは自分で実装します。
書き方としてはいろいろあると思いますが、例えば、以下のような形で書けると思います。
N = len(y)
T = 1000
with pm.Model() as model:
muZero = pm.Normal(name='muZero', mu=0.0, tau=1.0)
sigmaW = pm.InverseGamma(name='sigmaW', alpha=1.0, beta=1.0)
mu = [0]*N
mu[0] = pm.Normal(name='mu0', mu=muZero, tau=1/sigmaW)
for n in range(1, N):
mu[n] = pm.Normal(name='mu'+str(n), mu=mu[n-1], tau=1/sigmaW)
sigmaV = pm.InverseGamma(name='sigmaV', alpha=1.0, beta=1.0)
y_pre = pm.Normal('y_pre', mu=mu, tau=1/sigmaV, observed=y)
start = pm.find_MAP()
step = pm.NUTS()
trace = pm.sample(T, step, start=start)上記でモデルの構築・学習までを行っています。
Stanと違って全てPythonになり、書き方もPythonライクで分かりやすい感じがしますね。
推定値(サンプリング値)を得るには以下の通りです。
mu_samples = np.array([trace['mu'+str(i)] for i in range(N)])
pred = mu_samples.mean(axis=1)
mu_lower, mu_upper = np.percentile(mu_samples, q=[2.5, 97.5], axis=1)
plt.plot(list(range(len(y)+1)), list(y)+[None], color='black')
plt.plot(list(range(1, len(y)+1)), pred)
plt.fill_between(list(range(1, len(y)+1)), mu_lower, mu_upper, alpha=0.3)
plt.show()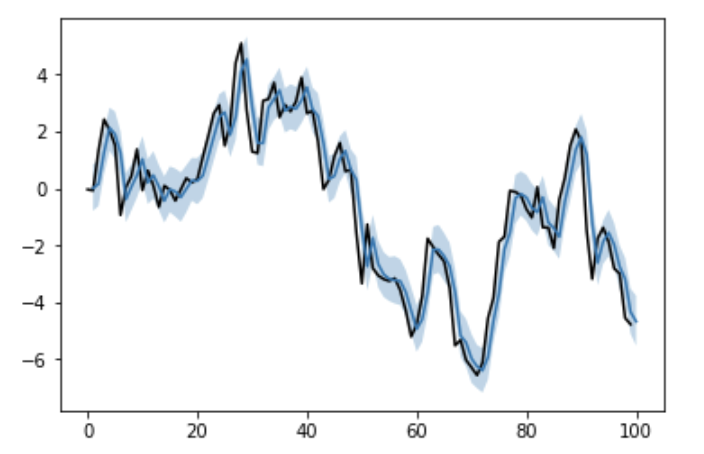
Edwardによる状態空間モデルの実装
Edwardでも、モデルを自前で実装する必要があります。
書き方は、Dustin氏(Edwardの開発をリード)のこの辺りのやりとりが参考になりました。
モデルの構築・学習のコードが以下の通り。
import tensorflow as tf
import edward as ed
from edward.models import Normal, InverseGamma, Empirical
N = len(y)
T = 1000
muZero = Normal(loc=0.0, scale=1.0)
sigmaW = InverseGamma(concentration=1.0, rate=1.0)
mu = [0]*N
mu[0] = Normal(loc=muZero, scale=sigmaW)
for n in range(1, N):
mu[n] = Normal(loc=mu[n-1], scale=sigmaW)
sigmaV = InverseGamma(concentration=1.0, rate=1.0)
y_pre = Normal(loc=tf.stack(mu), scale=sigmaV)
qmuZero = Empirical(tf.Variable(tf.zeros(T)))
qsigmaW = Empirical(tf.Variable(tf.zeros(T)))
qmu = [Empirical(tf.Variable(tf.zeros(T))) for n in range(N)]
qsigmaV = Empirical(tf.Variable(tf.zeros(T)))
latent_vars = {m: qm for m, qm in zip(mu, qmu)}
latent_vars[muZero] = qmuZero
latent_vars[sigmaW] = qsigmaW
latent_vars[sigmaV] = qsigmaV
inference = ed.HMC(latent_vars, data={y_pre: y})
inference.run(n_iter=T)近似事後分布を設定する辺りなどがEdward特有の書き方になりますが、それ以外はPyMCの書き方と似ているところがあります。
パラメータの値の取得も、以下のようにして取得できます。
良い感じに推定してくれてはいますが、信用区間が比較的広くなってしまいました。
PyStanと同じようにMCMCしたつもりですが、事前分布を自分で設定している辺りなどが影響があるのかもしれません。
または、収束判定などを入れていないはずなので、その辺りのせいかもしれません。
pred = np.zeros((len(y)), dtype=np.float32)
mu_lower = np.zeros((len(y)), dtype=np.float32)
mu_upper = np.zeros((len(y)), dtype=np.float32)
for i, _qmu in enumerate(tqdm(qmu)):
qmu_sample = _qmu.sample(1000).eval()
_pred = qmu_sample.mean()
_mu_lower, _mu_upper = np.percentile(qmu_sample, q=[2.5, 97.5], axis=0)
pred[i] = _pred
mu_lower[i] = _mu_lower
mu_upper[i] = _mu_upper
plt.plot(list(range(len(y)+1)), list(y)+[None], color='black')
plt.plot(list(range(1, len(y)+1)), pred)
plt.fill_between(list(range(1, len(y)+1)), mu_lower, mu_upper, alpha=0.3)
plt.show()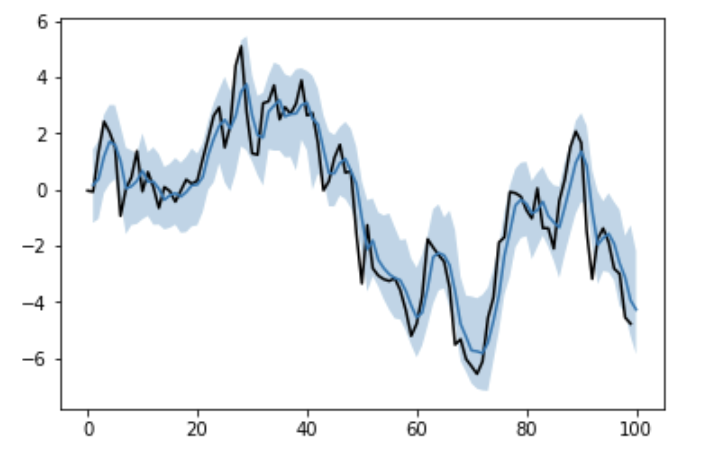
まとめ
今回は状態空間モデルの基本的な考え方と、Statsmodels、PyStan、PyMC、Edwardを使用した簡単なコーディング例について紹介しました。
状態空間モデルは、時系列データに対する強力なツールであり、潜在的な状態や隠れたパターンを推定する際に非常に有用です。
今回のように色々な手段でアプローチできると実務においても応用の機会の幅が広がります。
状態空間モデルの世界は広く深いため、今回紹介した内容だけで全てをカバーすることはできませんが、本記事が皆さんの勉強や実践に一歩でも役立てば幸いです。
