地理データ分析は公共政策や地域の発展、そして地域別のマーケティング施策に欠かせない役割を果たします。
地域別データを理解し適切なモデルで分析することで、それぞれの地域の特徴を把握することができます。
今回はe-Statという日本政府が調査した統計データをダウンロードできるサイトからデータを取得し、階層ベイズモデルを用いて地域別のデータ分析を行う方法について紹介します。
階層ベイズモデルでは異なる地域間の相違を考慮しながら統計モデルを構築することができ、より精緻な予測や洞察を得るのに役立ちます。
e-Stat APIによる政府統計データの取得
e-Statは、日本政府が調査した統計データを閲覧・ダウンロードできるように管理されたポータルサイトで、国立社会保障・人口問題研究所(IPSS)が運営している公式の統計データベースです。
国勢調査、経済統計、人口動態、労働統計、産業統計など、日本政府機関や関連組織によって収集された様々な統計情報を一括して提供することで、簡単なアクセスとデータの利用を可能にしています。
- e-Stat API : http://www.e-stat.go.jp/api/
e-Statは一般市民や研究者、企業など、誰でも無料でアクセスできるオープンなプラットフォームで、公共政策の策定や研究活動に役立てることが可能です。
ユーザー登録もメールアドレス・所属などを入力するだけ登録可能と、とても簡単です。
ユーザー登録をし、ログインをしますと、アプリケーションIDを取得するページに行くことができます。
APIを自分が公開しているWebサイトから利用したい場合は、そのWebサイトのURLを入力します。
今回のように試験的な利用目的なだけであればhttp://localhost/を入力しておけばOKです。
これで「発行」を押すと、「appId」にアプリケーションIDが発行されます。
これをリクエストパラメータで渡すことで、データを取得することが可能になります。
次章で実際にAPIを使って国勢調査のデータを取得して、マップに可視化するところまで見ていきましょう。
foliumによるマップ可視化
Pythonでマップを可視化するライブラリとしてfoliumというものがありますので、これを使います。
OpenStreetMapをJavascriptで表示するライブラリとしてLeaflet.jsというものがありますが、foliumはこれをPython上で動作させるもののようです。
さらにgeojsonやtopojsonを読み込むことができますので、日本の都道府県データのgeojsonとe-Stat APIからダウンロードして加工したデータフレームを紐付けて、このfoliumでLeaflet上に可視化することができます。
実際に、e-Stat APIから国勢調査の人口データを取得して、foliumで可視化するコード例が以下の通りです。
import numpy as np
import pandas as pd
import urllib.request
import folium
from IPython.display import display
appid = "YOUR APPLICATION ID"
api_version = "2.1"
base_url = "http://api.e-stat.go.jp/rest/{api_version}/app/".format(api_version=api_version)
"""
get_type = "getStatsList"
stats_code = "00200521" # 国勢調査
url = base_url + "{get_type}?appId={appid}&statsCode={stats_code}".format(
api_version=api_version,
get_type=get_type,
appid=appid,
stats_code=stats_code,
)
print(url) # 確認して取得したいデータのIDを調べる
"""
"""
get_type="getStatsData"
stats_data_id="0003148596" # 最新の調査ID
url = base_url + "{get_type}?appId={appid}&statsDataId={stats_data_id}".format(
api_version=api_version,
get_type=get_type,
appid=appid,
stats_data_id=stats_data_id
)
print(url) # 確認して取得したい項目パラメータを調べる
"""
# load data from e-stat api
get_type="getSimpleStatsData"
stats_data_id="0003148596"
cd_cat_01="0000" # 国籍->全て
cd_cat_02="0000" # 性別->男女
cd_cat_03="00710" # 集計地域->全域
lv_area="2" # 集計レベル->都道府県レベル
section_header_flg="2" # セクションヘッダー->無し
url = base_url + "{get_type}?appId={appid}&statsDataId={stats_data_id}&cdCat01={cd_cat_01}&cdCat02={cd_cat_02}&cdCat03={cd_cat_03}&lvArea={lv_area}§ionHeaderFlg={section_header_flg}".format(
api_version=api_version,
get_type=get_type,
appid=appid,
stats_data_id=stats_data_id,
cd_cat_01=cd_cat_01,
cd_cat_02=cd_cat_02,
cd_cat_03=cd_cat_03,
lv_area=lv_area,
section_header_flg=section_header_flg,
)
d = urllib.request.urlopen(url).read().decode("utf8")
dlines = d.splitlines()[2:]
jcodes = []
names = []
populations = []
for line in dlines:
line2 = line.replace('"', "").split(",")
jcode = line2[8]
name = line2[9]
population = line2[13]
jcode = jcode[0:2]
population = int(population)
jcodes.append(jcode)
names.append(name)
populations.append(population)
df = pd.DataFrame({"jcode" : jcodes, "name" : names, "population" : populations})
display(df)
# create leaflet map by folium
location = [39.702053, 141.15448379999998]
tiles="Stamen Toner"
zoom_start = 5
map = folium.Map(location=location, tiles=tiles, zoom_start=zoom_start)
map.choropleth(
geo_path="japan.geojson",
data=df,
columns=["jcode", "population"],
key_on="properties.JCODE",
threshold_scale=[10000, 50000, 100000, 150000, 200000, 300000],
fill_color="YlGnBu", fill_opacity=0.7, line_opacity=0.2)
display(map)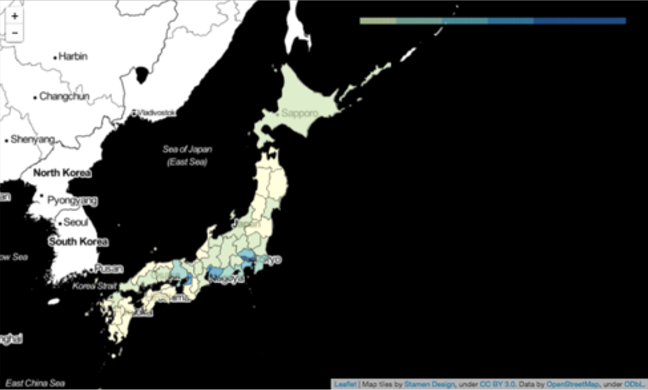
e-Stat公式ページの「提供データ」によれば、統計表情報取得「getStatsList」で統計表情報取得ができ、パラメータの政府統計コードは、例えば「国勢調査」は上記コードの通り「00200521」とのこと。
これをリクエストパラメータに設定してあげてアクセスすると、これまでに調査された国勢調査のデータ一覧が確認できます。
取得したい国勢調査のデータのデータIDを確認して、統計データ取得「getStatsData」でアクセスすると、項目などの情報とデータが取得できます。
今回は、項目の絞り込みなどのパラメータも確認して「getSimpleStatsData」でCSVで取得することにし、適当にデータフレーム化しておく形にしました。
階層ベイズモデルによる地域別自殺リスクの推定
さて、この章では本題である、階層ベイズモデルによる地域別データ分析とその可視化の例をご紹介します。
具体的には、以下の書籍の中でe-Statから取得した地理データから階層ベイズモデルを用いて地域特徴を推定する事例を紹介されており、これを真似してみます。
ただし、上記書籍では、e-Statから普通にダウンロードしたデータを、Stan/BUGSなどのベイズ統計言語でデータを推定し、そこからまた別の地理データ可視化ソフトウェアを使って、推定結果を可視化しています。
今回はそれらを全てPythonで一括してやってみようと思います。
上記書籍でやっていることはより具体的には、地図上に表現された地理的な隣接情報を利用して、空間的な相関を考慮した階層ベイズモデルを用いた「地域別の自殺リスク」の推定を行って、その結果をコロプレスマップとして地図上に可視化、ということをやっています。
e-Statでダウンロードした地域別の自殺数を用いて普通に自殺リスクを算出しようとすると、地域によっては値が小さすぎて適切な自殺リスクが得られないため、ベイズモデルで空間的な相関を導入することでこれを解決するという方法を提案しています。
「自殺リスク」とは何かという話ですが、これについては疫学の分野において、ある基準集団と比べて相対的にリスクが高いか低いかを表す指標で、標準化死亡比(SMR)というものがあります。
ある地区が基準集団と同じリスクを持つ場合の死亡数のことを期待死亡数と呼び、下記で計算できます。
\(\text{期待死亡数}\hspace{0.5em}y=\displaystyle\sum_i{\Bigl(}n_i\frac{Z_i}{N_i}{\Bigr)}\)
\(Z_i : \text{基準集団での年齢}i\text{の死亡数}\)
\(N_i : \text{基準集団の年齢}i\text{の人口}\)
\(n_i : \text{その地域の年齢}i\text{の人口}\)
観測された死亡数がこの期待死亡数に比べて多い場合死亡のリスクが大きいと考えられ、これを標準化死亡比(SMR)と言います。
\(SMR=\displaystyle\frac{z}{y}\)
\(z : \text{観測死亡数}\)
データからこの比率を単純に計算することもできますが、今回はこれを推定する方向で実装します。
上記を踏まえて、SMRを地域の相関が考慮されるように推定する階層ベイズモデルを次のように設計します。
\(z_i{\sim}Poisson(\lambda_i)\)
\(\lambda_i=y_i\exp(\phi_i+\psi_i)\)
\(\phi_i{\sim}N(0,\sigma^2)\)
\(\psi_i|\psi_{j{\neq}i}{\sim}N\Bigl(\displaystyle\frac{1}{m_i}\displaystyle\sum_{j{\in}n(i)}\psi_i,\displaystyle\frac{1}{m_i}\sigma^2_{\psi}\Bigr)\)
\(z_i : \text{地区}i\text{の死亡数}\)
\(y_i : \text{地区}i\text{の期待死亡数}\)
\(\phi_i : \text{地区}i\text{固有の効果を表すパラメータ}\)
\(\psi_i : \text{地区}i\text{は隣接地区と似通った傾向を持つことを表すパラメータ}\)
データは死亡数なのでポアソン対数正規モデルとし、ポアソン分布のパラメータに地域相関のあるSMRがかかる形にしています。
ここで\(\exp(\phi_i+\psi_i)\)が地区\(i\)のSMRの推定値に相当します。
上記の統計モデルをPythonで定義してみます。
個人的にはPyStanの方が好みですが、今回はPyMCを使ってみます。
PyMCにはPyMC2系列とPyMC3系列があり、PyMC3の方を使います。
PyMCの方はコードはスマートになりやすく、モデルの構造も直感的に分かりやすい反面、ネット上の情報はやはりStanの方が多いといったメリデメがあります。
前述同様にデータはe-Stat APIから直接取得し、ベイズ推定はPyMC3で行い、推定結果をfoliumでマップ上に可視化してみるコードは以下の通りです。
import re
import csv
import numpy as np
import pandas as pd
import urllib.request
import folium
from IPython.display import display
import pymc3 as pm
%matplotlib inline
import matplotlib.pylab as plt
appid = "YOUR APPLICATION ID"
api_version = "2.1"
base_url = "http://api.e-stat.go.jp/rest/{api_version}/app/".format(api_version=api_version)
get_type = "getStatsList"
#stats_code = "00450011" # 人口動態調査
#stats_code = "00200524" # 人口推計
#stats_code = "00200521" # 国勢調査
#print(base_url + "{}?appId={}&statsCode={}".format(get_type, appid, stats_code))
# 都道府県別の自殺数
get_type="getStatsData"
stats_data_id="0003030127"
url =base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)
get_type="getSimpleStatsData"
stats_data_id="0003030127"
lv_cat_01="2"
cd_cat_02="129"
cd_cat_03="1"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&lvCat01={}&cdCat02={}&cdCat03={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, lv_cat_01, cd_cat_02, cd_cat_03, section_header_flg)
data_pref_die = urllib.request.urlopen(url).read().decode("utf8")
# 都道府県別、年齢階級別の人口
get_type="getStatsData"
stats_data_id="0003014716"
url = base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)
get_type="getSimpleStatsData"
stats_data_id="0003014716"
cd_cat_01="000"
cd_cat_02_from="01001"
cd_cat_02_to="04018"
lv_area="2"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&cdCat01={}&cdCat02From={}&cdCat02To={}&lvArea={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, cd_cat_01, cd_cat_02_from, cd_cat_02_to, lv_area, section_header_flg)
data_pref_age_pop = urllib.request.urlopen(url).read().decode("utf8")
# 全国、年齢階級別の自殺数
get_type="getStatsData"
stats_data_id="0003031497"
url =base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)
get_type="getSimpleStatsData"
stats_data_id="0003031497"
lv_cat_01="2"
cd_cat_02="268"
cd_cat_03="1"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&lvCat01={}&cdCat02={}&cdCat03={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, lv_cat_01, cd_cat_02, cd_cat_03, section_header_flg)
data_all_age_die = urllib.request.urlopen(url).read().decode("utf8")
# 全国、年齢階級別の人口
get_type="getStatsData"
stats_data_id="0003014709"
url = base_url + "{}?appId={}&statsDataId={}".format(get_type, appid, stats_data_id)
#print(url)
get_type="getSimpleStatsData"
stats_data_id="0003014709"
cd_cat_01 = "000"
cd_cat_02 = "001"
cd_cat_03_from = "01001"
cd_cat_03_to = "01021"
cd_time = "2009000000"
section_header_flg="2"
url = base_url + "{}?appId={}&statsDataId={}&cdCat01={}&cdCat02={}&cdCat03From={}&cdCat03To={}&cdTime={}§ionHeaderFlg={}".format(get_type, appid, stats_data_id, cd_cat_01, cd_cat_02, cd_cat_03_from, cd_cat_03_to, cd_time, section_header_flg)
data_all_age_pop = urllib.request.urlopen(url).read().decode("utf8")
# 都道府県別の自殺数、データフレーム化
dlines = data_pref_die.splitlines()[2:]
jiscode, cnt = [], []
for line in dlines:
line2 = line.replace('"', "").split(",")
jiscode_tmp = line2[2]
jiscode_tmp = int(jiscode_tmp)-1
if jiscode_tmp > 47:
continue
jiscode_tmp = "0" + str(jiscode_tmp) if jiscode_tmp < 10 else str(jiscode_tmp)
jiscode.append(jiscode_tmp)
cnt_tmp = int(line2[11])
cnt.append(cnt_tmp)
df_pref_die = pd.DataFrame({"jiscode": jiscode, "cnt": cnt})
# 都道府県コードマスタ、都道府県別、年齢階級別の人口、データフレーム化
dlines = data_pref_age_pop.splitlines()[2:]
jiscode, name, age_cls, cnt = [], [], [], []
for line in dlines:
line2 = line.replace('"', "").split(",")
jiscode_tmp = line2[6]
jiscode_tmp = jiscode_tmp.replace("000", "")
jiscode.append(jiscode_tmp)
name_tmp = line2[7]
name.append(name_tmp)
age_cls_tmp = line2[5]
age_cls_tmp = age_cls_tmp.replace("歳", "").split("~")
age_cls_tmp = "85_" if len(age_cls_tmp) == 1 else age_cls_tmp[0]+"_"+age_cls_tmp[1]
age_cls.append(age_cls_tmp)
cnt_tmp = line2[11]
cnt_tmp = int(cnt_tmp)*1000
cnt.append(cnt_tmp)
df_pref_age_pop = pd.DataFrame({"jiscode": jiscode, "age_cls": age_cls, "cnt": cnt})
df_pref_age_pop_14 = df_pref_age_pop.query("age_cls=='0_4' | age_cls=='5_9' | age_cls=='10_14'")
df_pref_age_pop_14 = df_pref_age_pop_14[["jiscode", "cnt"]].groupby("jiscode").sum().reset_index()
col14 = pd.DataFrame([["_14"]*47]).T
col14.columns = ["age_cls"]
df_pref_age_pop_14 = pd.concat([df_pref_age_pop_14, col14], axis=1)
df_pref_age_pop = df_pref_age_pop.query("age_cls!='0_4' & age_cls!='5_9' & age_cls!='10_14'")
df_pref_age_pop = pd.concat([df_pref_age_pop, df_pref_age_pop_14], axis=0)
jiscode = sorted(set(jiscode), key=jiscode.index)
name = sorted(set(name), key=name.index)
df_pref_mst = pd.DataFrame({"jiscode": jiscode, "name": name})
# 全国の年齢階級別の自殺数、データフレーム化
dlines = data_all_age_die.splitlines()[2:]
age_cls, cnt = [], []
for line in dlines:
line2 = line.replace('"', "").split(",")
age_cls_tmp = line2[3]
if age_cls_tmp == "不詳":
continue
age_cls_tmp = re.sub(r"歳|~", "", age_cls_tmp)
age_cls_tmp = "100_" if age_cls_tmp == "100" else str(int(age_cls_tmp.split("-")[0]))+"_"+str(int(age_cls_tmp.split("-")[-1]))
age_cls.append(age_cls_tmp)
cnt_tmp = line2[-1]
cnt_tmp = 0 if cnt_tmp == "-" else int(cnt_tmp)
cnt.append(cnt_tmp)
age_cls = age_cls[3:-3]
age_cls.insert(0, "_14")
age_cls[-1] = "85_"
cnt_15 = np.sum(cnt[0:3])
cnt_85 = np.sum(cnt[-4:])
cnt = cnt[3:-4]
cnt.insert(0, cnt_15)
cnt.append(cnt_85)
df_all_age_die = pd.DataFrame({"age_cls" : age_cls, "cnt" : cnt})
# 全国の年齢階級別の人口、データフレーム化
dlines = data_all_age_pop.splitlines()[2:]
age_cls, cnt = [], []
for line in dlines:
line2 = line.replace('"', "").split(",")
age_cls_tmp = line2[5]
age_cls_tmp = re.sub(r"歳", "", age_cls_tmp).split("~")
age_cls_tmp = "100_" if len(age_cls_tmp) == 1 else age_cls_tmp[0]+"_"+age_cls_tmp[1]
age_cls.append(age_cls_tmp)
cnt.append(int(line2[-1])*1000)
age_cls = age_cls[3:-3]
age_cls.insert(0, "_14")
age_cls[-1] = "85_"
cnt_15 = np.sum(cnt[0:3])
cnt_85 = np.sum(cnt[-4:])
cnt = cnt[3:-4]
cnt.insert(0, cnt_15)
cnt.append(cnt_85)
df_all_age_pop = pd.DataFrame({"age_cls" : age_cls, "cnt" : cnt})
# 都道府県別、期待死亡数、データフレーム
df_y_tmp = pd.merge(df_all_age_pop, df_all_age_die, how="inner", on="age_cls", suffixes=("_pop", "_die"))
df_y_tmp = df_y_tmp.assign(y_tmp=df_y_tmp["cnt_die"]/df_y_tmp["cnt_pop"])
df_y_tmp = df_y_tmp.drop("cnt_pop", axis=1).drop("cnt_die", axis=1)
df_y_tmp = pd.merge(df_pref_age_pop, df_y_tmp, how="inner", on="age_cls")
df_y_tmp = df_y_tmp.assign(y=df_y_tmp["y_tmp"]*df_y_tmp["cnt"])
df_y_tmp = df_y_tmp.drop("cnt", axis=1).drop("y_tmp", axis=1)
df_y = df_y_tmp[["jiscode", "y"]].groupby("jiscode").sum().reset_index()
# 都道府県別、隣接都道府県、データフレーム
from_names, to_names = [], []
with open("japan_adj.csv", "r") as f:
reader = csv.reader(f)
for row in reader:
from_name_tmp = row[1].replace("\xa0", "").replace(" ", "")
to_names_tmp = row[4].replace("\xa0", "").replace(" ", "").split(",")
for to_name_tmp in to_names_tmp:
from_names.append(from_name_tmp)
to_names.append(to_name_tmp)
from_names = from_names[0:-1]
to_names = to_names[0:-1]
df_adj_tmp = pd.DataFrame({"f_name": from_names, "t_name": to_names})
df_adj_tmp = pd.merge(df_adj_tmp, df_pref_mst, how="left", left_on="f_name", right_on="name").drop("name", axis=1).rename(columns={"jiscode": "f_jiscode"})
df_adj_tmp = pd.merge(df_adj_tmp, df_pref_mst, how="left", left_on="t_name", right_on="name").drop("name", axis=1).rename(columns={"jiscode": "t_jiscode"})
df_adj = df_adj_tmp.drop("f_name", axis=1).drop("t_name", axis=1)
# 自殺数、期待死亡数、隣接行列 for 階層ベイズモデル
jiscodes = list(df_pref_mst["jiscode"].values.flatten())
n = len(jiscodes)
y_samples, z_samples, adj_matrix, d_matrix = [], [], [], []
for i in range(0, n):
y = df_y[df_y["jiscode"] == jiscodes[i]]["y"].values[0] # 期待死亡数
y_samples.append(y)
z = df_pref_die[df_pref_die["jiscode"] == jiscodes[i]]["cnt"].values[0] # 自殺数
z_samples.append(z)
adjs = df_adj[df_adj["f_jiscode"] == jiscodes[i]]["t_jiscode"].values # 隣接JISCODE
adjs_idx = np.zeros(n)
for j in adjs:
adjs_idx[jiscodes.index(j)] = 1
adj_matrix.append(adjs_idx)
d_idx = np.zeros(n)
d_idx[i] = 2
d_matrix.append(d_idx)
jiscodes = np.array(jiscodes, dtype=object) # JISCODE
y_samples = np.array(y_samples, dtype=int) # 期待死亡数
z_samples = np.array(z_samples, dtype=int) # 自殺数
adj_matrix = np.array(adj_matrix, dtype=int).reshape(n, n) # 隣接行列
d_matrix = np.array(d_matrix, dtype=int).reshape(n, n) # 自身の行列
# ベイズモデルで推定
with pm.Model() as model:
p1 = pm.Uniform("p1", lower=0, upper=1)
p2 = pm.Uniform("p2", lower=0, upper=1)
tau_phi = pm.Gamma("tau_phi", alpha=0.5, beta=0.005)
phi = pm.Normal("phi", mu=0, tau=tau_phi)
t = p1*d_matrix+p2*adj_matrix
psi = pm.MvNormal('psi', mu=0, cov=t, shape=n)
lamb = np.exp(np.log(y_samples)+phi+psi)
z = pm.Poisson("z", mu=lamb, observed=z_samples)
start = pm.find_MAP()
step = pm.NUTS()
trace = pm.sample(1000, step, start)
#pm.traceplot(trace)
#pm.summary(trace)
phi_m = np.mean(trace["phi"])
psi_m = []
t = trace["psi"].transpose()
for i in t:
psi_m.append(np.mean(i))
smr_est = np.exp(phi_m+psi_m)
# 都道府県別、推定SMR
df_smr_est = pd.DataFrame({"jiscode" : jiscodes, "smr_est" : smr_est})
display(df_smr_est)
# コロプレスマップに推定値を可視化
location = [35.709634, 139.392101]
tiles="Stamen Toner"
zoom_start = 10
map = folium.Map(location=location, tiles=tiles, zoom_start=zoom_start)
map.choropleth(
geo_path="japan.geojson",
data=df_smr_est,
columns=["jiscode", "smr_est"],
key_on="properties.JCODE",
threshold_scale=[0.90, 0.95, 1.00, 1.05, 1.10, 1.15],
fill_color="YlGnBu",
fill_opacity=0.7,
line_opacity=0.3,
reset=True)
display(map)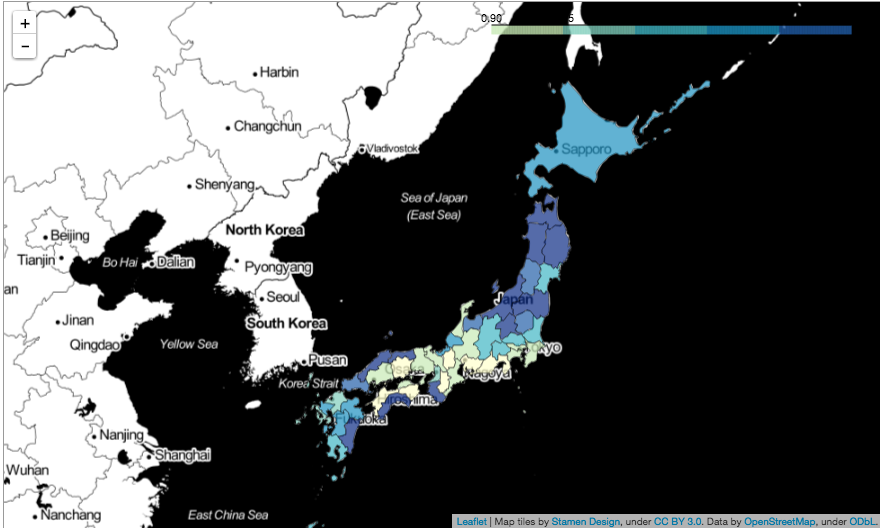
都道府県別でリスク推定をしてみた結果になります。
思ったよりも、地方の方がリスクが高いように推定されているみたいで、期待死亡数の方も全体的に地方の方が高い傾向にありました。
まとめ
今回は、日本の統計ポータルサイトであるe-Statから地域別統計データをダウンロードし、階層ベイズモデルを使用してデータ分析を行う方法を紹介しました。
e-Statのオープンアクセス性と豊富なデータは、地域の発展や社会的な課題解決に向けた有益な知見を提供してくれます。
e-Stat APIは設定が細かく使い方が少々難易度が高いため、初めての人はまずはAPIを介さず普通にデータをダウンロードして感覚を得ながら活用してみることをおすすめします。
また、階層ベイズモデルを適用することで、地域間の違いや地域間の関係を考慮した予測が可能となることも示せました。
余談ですが、PyMC3は普段あまり使っておらず、今回は大変実装の勉強になりました。
ただ、個人的には、地域相関を入れるCAR事前モデルの部分が、Stanですとパッケージで自動的にやってくれるみたいですが、PyMCはそれがないので自前で作らなければならず、そこが正しく出来ているのか不安です。
特に、多変量ガウス分布の分散共分散行列で地域相関を表現させる際の重みの調整はどうすれば良いか分からず、結局そこにも事前分布を入れて、回してみるようにしてみた、といったところです。
