世の中がデータ駆動の時代に突入し、一切の情報がデジタル化されていく中で、私たちは日々膨大な量のデータと向き合っています。
その結果、データから意味ある情報を引き出し、より良い意思決定を行うために数理最適化がますます重要なツールとなってきています。
今回は、そんな数理最適化の中でもPythonを用いた実装に焦点を当ててみます。
具体的には、PuLPというライブラリを用いた数理最適化の一例として、巡回セールスマン問題と運搬経路問題の解法をご紹介します。
さらに、一歩先を行くための新しいアプローチとして、深層強化学習を利用したTSPの解法についても触れてみたいと思います。
PuLPについて
PuLPは、線形計画問題(Linear Programming Problem: LP)・混合整数計画問題(Mixed Integer Programming Problem: MIP)をPythonでモデル化し、ソルバーを使って解くためのPythonライブラリです。
公式サイトは以下になります。
- https://coin-or.github.io/pulp/index.html
- https://pypi.org/project/PuLP
- https://github.com/coin-or/pulp
PuLPそのものは、最適化問題をモデル化する役割を持っており、モデラーと呼ばれたりします。
一方、ソルバーは、与えられたモデルの制約条件に従い、目的関数の最適解を解析するソフトウェアです。
PuLPインストール時に同時にデフォルトのソルバーであるCBCもインストールされます。
PuLPで最適化問題を解くとき、内部では以下のフローが実行されます。
- PuLPで最適化問題をモデル化し、.mpsファイルとして出力 (PuLPが実行)
- .mpsファイルを読み込んで、問題を解く (ソルバーが実行)
- 最適解を.solファイルとして出力 (ソルバーが実行)
- .solファイルを読み込んで、最適解をPython内の変数に格納する (PuLPが実行)
ソルバーはCBC以外にも、以下のようなツールを別途購入・インストールして、PuLPから使用することができます。
| ソルバー名 | 有料/無料 | 強み | 弱み |
|---|---|---|---|
| CBC | 無料 | 柔軟性あり 独自の機能を追加可能 | 商用ソルバーより性能が劣る 大規模問題には不向き |
| GLPK | 無料 | オープンソース 幅広い最適化問題に利用可能 | 商用ソルバーより性能が劣る 大規模問題には不向き |
| SCIP | 無料 (学術利用のみ) | 高性能 柔軟なモデリングオプション | 初期設定が複雑 学習コストが高い |
| Gurobi | 有料 | 高性能 多機能 産業界で広く使用 優れたサポート | ライセンス費用が発生 |
| CPLEX | 有料 | 高性能 信頼性高い 産業界で広く使用 充実したドキュメンテーション | 初期設定が複雑 ライセンス費用が発生する |
この後にPuLPを使ったコード例をご紹介しますが、その他にも以下の書籍らは、基本的な最適化問題をPuLPで解くコードも記載されているのでお勧めです。
巡回セールスマン問題(TSP)とPuLPによる解法
巡回セールスマン問題(Traveling Salesman Problem: TSP)とは、ある都市から出発してすべての都市を1度ずつ訪れて、元の都市に戻ることを考えたときに、総移動距離が一番最短となるルートを求める最適化問題です。
組み合わせ最適化問題の代表的な問題の1つで、NP困難と呼ばれる問題のクラスに属します。
都市の数が増えるほど、組み合わせ候補数が爆発的に増えるため、計算量的に解析が困難になる問題です。
これをPuLPを使って混合整数計画法で解いてみます。
今回の問題となるデータは以下のように自前で作成します。
# Define TSP
n_customer = 9
n_point = n_customer + 1
df = pd.DataFrame({
'x': np.random.randint(0, 100, n_point),
'y': np.random.randint(0, 100, n_point),
})
df.iloc[0]['x'] = 0
df.iloc[0]['y'] = 0n_customerで都市(訪問するクライアント)の数を設定し、各都市の座標\(x,y\)を乱数でランダムに振り分けて作成しました。
ただし、最初の1点だけは出発する都市(DEPOT)とします。
DEPOTからスタートして、これらの点をすべて経由して、DEPOTに戻る最短経路を求めてみます。
まずは各都市がどのような配置関係になっているのかを可視化して見てみます。
# Check TSP state
plt.figure(figsize=(5, 5))
# Draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
plt.text(row['x'] + 1, row['y'] + 1, f'{i}')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id')
plt.show()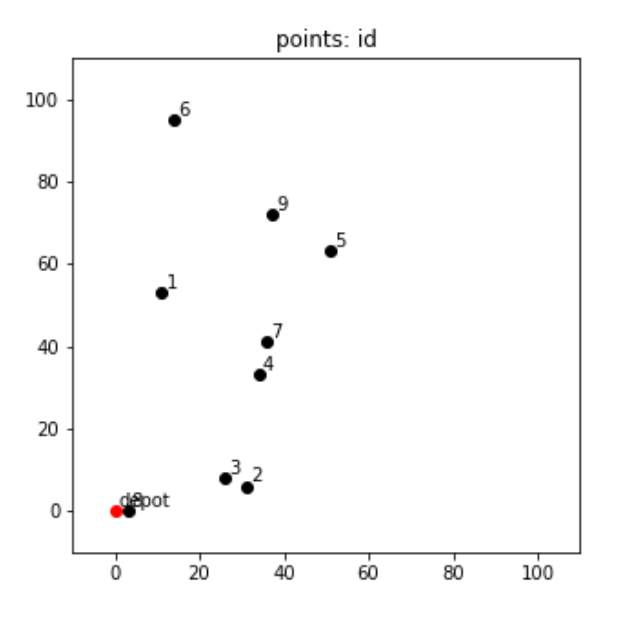
ちょっと全体的に左側に寄ってしまいましたが、このまま行きましょう。
これを解くためのPuLPの実装が以下のようになります。
# Set the problem
problem = pulp.LpProblem('tsp_mip', pulp.LpMinimize)
# Set valiables
x = pulp.LpVariable.dicts('x', ((i, j) for i in range(n_point) for j in range(n_point)), lowBound=0, upBound=1, cat='Binary')
# We need to keep track of the order in the tour to eliminate the possibility of subtours
u = pulp.LpVariable.dicts('u', (i for i in range(n_point)), lowBound=1, upBound=n_point, cat='Integer')
# Set the objective function
problem += pulp.lpSum(distances[i][j] * x[i, j] for i in range(n_point) for j in range(n_point))
# Set constrains
for i in range(n_point):
problem += x[i, i] == 0
for i in range(n_point):
problem += pulp.lpSum(x[i, j] for j in range(n_point)) == 1
problem += pulp.lpSum(x[j, i] for j in range(n_point)) == 1
# eliminate subtour
for i in range(n_point):
for j in range(n_point):
if i != j and (i != 0 and j != 0):
problem += u[i] - u[j] <= n_point * (1 - x[i, j]) - 1
# Solve the problem
status = problem.solve()
# Output status, value of objective function
status, pulp.LpStatus[status], pulp.value(problem.objective)
(1, 'Optimal', 240.18288657336905)# Set variablesパートにおいて、\(x_{i,j}\)が\(i\) から\(j\)に移動する場合は1, そうでない場合は0とする決定変数を用意しています。# Set the object functionパートにて、\(x_{i,j}=1\)の場合にその区間の距離\(distance_{i,j}\)をかけて総移動距離を計算し、これを最小化しています。
また、# Set constrainsのパートでは、同じ都市への移動はありませんので、\(x_{i, i} = 0\)とし、都市間の区間は必ず1回だけ通るという制約を入れています。
最適化された巡回経路を可視化してみるコードと図は以下のような感じになりました。
# Check TSP problem and optimized route
plt.figure(figsize=(5, 5))
# Draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
plt.text(row['x'] + 1, row['y'] + 1, f'{i}')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id')
# Draw optimal route
routes = [(i, j) for i in range(n_point) for j in range(n_point) if pulp.value(x[i, j]) == 1]
arrowprops = dict(arrowstyle='->', connectionstyle='arc3', edgecolor='blue')
for i, j in routes:
plt.annotate('', xy=[df.iloc[j]['x'], df.iloc[j]['y']], xytext=[df.iloc[i]['x'], df.iloc[i]['y']], arrowprops=arrowprops)
plt.show()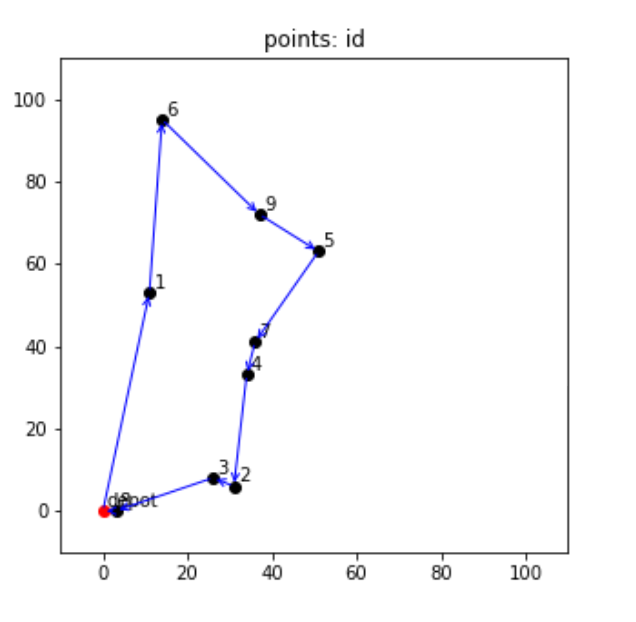
ここで一度コードの中の# eliminate subtourの部分に戻りますが、これは何をしているかというと、部分巡回経路ができてしまわないように制御しています。
すなわち、問題としては一筆書きのように経路を求めてほしいのです。
この制約がないと、別に飛び飛びでも最短経路は計算できるよね?ということで、以下のような解を求めてしまうことになります。
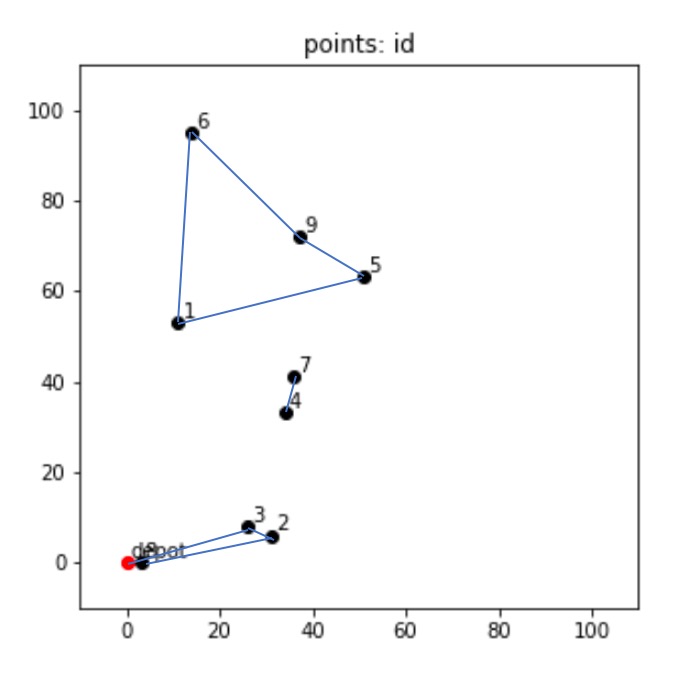
以上を踏まえ、問題解析後のステータスpulp.LpStatus[status]はOptimalで最適解が見つかったということになり、最適化された目的関数の値は240.18となりました。
運搬経路問題(VRP)とPuLPによる解法
運搬経路問題(Vehicle Routing Problem: VRP)は、TSPの一般化問題の一種で、複数の車両で複数の場所を訪れて荷物の集荷or配達をするときに、その総移動距離を最小化するような経路を求める問題です。
TSPよりも少し実用的になりました。
このような運搬経路を実用的な観点で考え、他にも様々な前提条件を考えて派生した問題はいくつもあります。
| 問題名 | 内容 |
|---|---|
| Capacitated VRP: CVRP | 車両の積載量に制約がある |
| VRP with Time Windows: VRPTW | 何時から何時までの間に集荷or配達しなければならないという時間帯の制約がある |
| Distance Constrained VRP: DCVRP | 車両が走行できる距離に制約がある |
| Multi Depots VRP: MDVRP | 車両が出発・到着できる拠点が複数ある |
| VRP with Pick-up and Delivery: VRPPD | 集荷→配達(ある拠点で集荷した荷物を、ある拠点に配達する)という制約がある |
この辺りをサーベイしている資料はいくつかありますが、今回は本題じゃありませんので、今回は積載キャパシティがあるVRP(CVRP)をPuLPを使って解いてみます。
先ほどと同様に、各拠点の座標と、その場所から運んでもらいたい需要demandのデータを自前で作成します。
# Define VRP
n_customer = 9
n_point = n_customer + 1
vehicle_capacity = 8
df = pd.DataFrame({
'x': np.random.randint(0, 100, n_point),
'y': np.random.randint(0, 100, n_point),
'demand': np.random.randint(1, 5, n_point),
})
df.iloc[0]['x'] = 0
df.iloc[0]['y'] = 0
df.iloc[0]['demand'] = 0各拠点の位置関係と需要を可視化するコードと図は以下の通りです。
# Check VRP state
plt.figure(figsize=(5, 5))
# Draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
demand = row['demand']
plt.text(row['x'] + 1, row['y'] + 1, f'{i}({demand})')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id(demand)')
plt.show()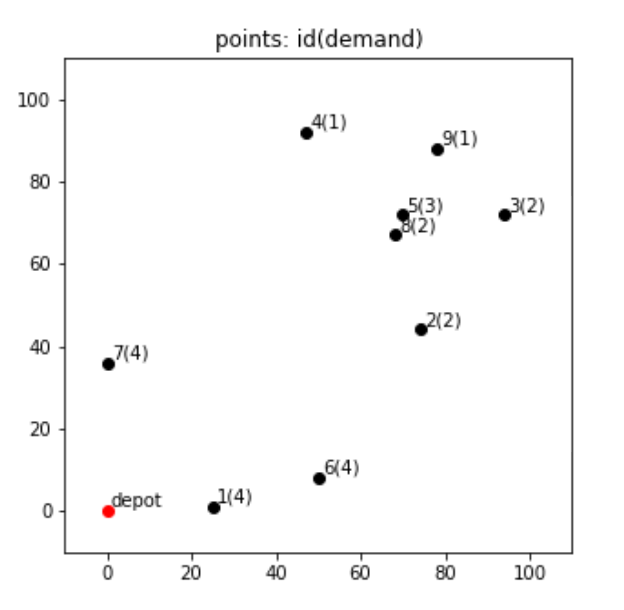
これを積載キャパシティ8の車両を使って、総移動距離を最小化したときに必要な台数およびそれぞれの運搬経路を求めるコード例が以下の通りです。
demands = df['demand'].values
# Set the problem
problem = pulp.LpProblem('cvrp_mip', pulp.LpMinimize)
# Set variables
x = pulp.LpVariable.dicts('x', ((i, j) for i in range(n_point) for j in range(n_point)), lowBound=0, upBound=1, cat='Binary')
n_vehicle = pulp.LpVariable('n_vehicle', lowBound=0, upBound=100, cat='Integer')
# Set the objective function
problem += pulp.lpSum([distances[i][j] * x[i, j] for i in range(n_point) for j in range(n_point)])
# Set constrains
for i in range(n_point):
problem += x[i, i] == 0
for i in range(1, n_point):
problem += pulp.lpSum(x[j, i] for j in range(n_point)) == 1
problem += pulp.lpSum(x[i, j] for j in range(n_point)) == 1
problem += pulp.lpSum(x[i, 0] for i in range(n_point)) == n_vehicle
problem += pulp.lpSum(x[0, i] for i in range(n_point)) == n_vehicle
# eliminate subtour
subtours = []
for length in range(2, n_point):
subtours += itertools.combinations(range(1, n_point), length)
for st in subtours:
demand = np.sum([demands[s] for s in st])
arcs = [x[i, j] for i, j in itertools.permutations(st, 2)]
problem += pulp.lpSum(arcs) <= np.max([0, len(st) - np.ceil(demand / vehicle_capacity)])
# Solve the problem
status = problem.solve()
# Output status, value of objective function
status, pulp.LpStatus[status], pulp.value(problem.objective)(1, 'Optimal', 598.2419050203686)
全体的にTSPのときと定式化が似ていることがわかると思います。
新しく追加された要素として主に2つあり、まずは以下の部分で、使っている車両の台数の辻褄を合わせています。(出ていく車両と帰ってくる車両の数を合わせる)
problem += pulp.lpSum(x[i, 0] for i in range(n_point)) == n_vehicle
problem += pulp.lpSum(x[0, i] for i in range(n_point)) == n_vehicleまた、次の部分で、需要と車両のキャパシティ制約を守っています。
for st in subtours:
demand = np.sum([demands[s] for s in st])
arcs = [x[i, j] for i, j in itertools.permutations(st, 2)]
problem += pulp.lpSum(arcs) <= np.max([0, len(st) - np.ceil(demand / vehicle_capacity)])
上記で解析した結果、総移動距離は598.24となり、使用する車両台数は3となりました。
最適化された結果を可視化してみるコードと図は以下のようになります。
# Check TSP problem and optimized route
plt.figure(figsize=(5, 5))
# Draw problem state
for i, row in df.iterrows():
if i == 0:
plt.scatter(row['x'], row['y'], c='r')
plt.text(row['x'] + 1, row['y'] + 1, 'depot')
else:
plt.scatter(row['x'], row['y'], c='black')
demand = row['demand']
plt.text(row['x'] + 1, row['y'] + 1, f'{i}({demand})')
plt.xlim([-10, 110])
plt.ylim([-10, 110])
plt.title('points: id(demand)')
# Draw optimal route
cmap = matplotlib.cm.get_cmap('Dark2')
routes = [(i, j) for i in range(n_point) for j in range(n_point) if pulp.value(x[i, j]) == 1]
for v in range(int(pulp.value(n_vehicle))):
# identify the route of each vehicle
vehicle_route = [routes[v]]
while vehicle_route[-1][1] != 0:
for p in routes:
if p[0] == vehicle_route[-1][1]:
vehicle_route.append(p)
break
# draw for each vehicle
arrowprops = dict(arrowstyle='->', connectionstyle='arc3', edgecolor=cmap(v))
for i, j in vehicle_route:
plt.annotate('', xy=[df.iloc[j]['x'], df.iloc[j]['y']], xytext=[df.iloc[i]['x'], df.iloc[i]['y']], arrowprops=arrowprops)
plt.show()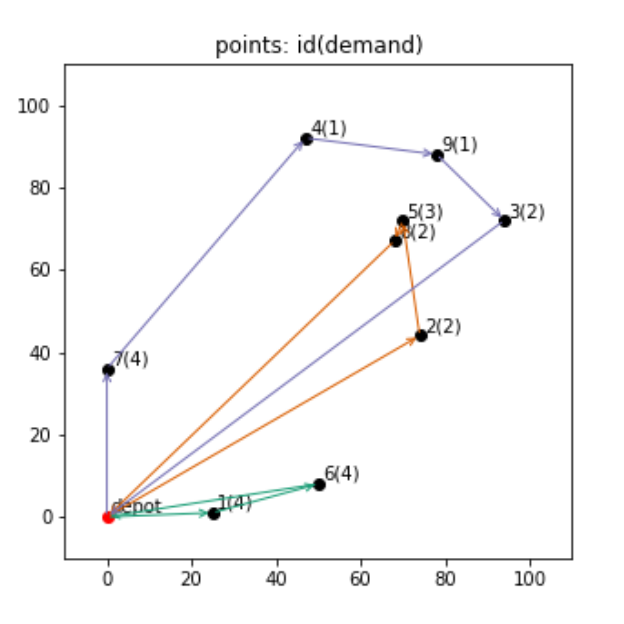
それぞれの色が車両を表し、3台を使って図のように回ってもらう経路が、総移動距離を最小化する経路とのことです。
こうしてみると、今回は割と各車両の走行距離に差がある結果になっています。
もし現実的にそれぞれの車両の移動距離や稼働時間に制約があるとか、車両ごとにかかるコストが異なるなどがあれば、それをまた定式化に加えてモデルを再構築するなどの工夫をする必要があります。
深層強化学習によるアプローチについて
これまでのご紹介したTSPやVRPのような一般的な問題には、これまでに記したように、最適化手法を使って解きます。
一方で、近年ではニューラルネットワークや深層学習が発展したことにより、深層強化学習を使って最適化問題にアプローチする方法も提案されています。
そのような手法を使う場合はどのような実装になるのか、TSPを例に実装してみましたので、それについて記します。
深層学習モデルのアーキテクチャはPointer Networkと呼ばれるモデルを試しました。
- Pointer Network: https://arxiv.org/abs/1506.03134
Pointer Networkは2017年にGoogleが出した論文で提案されたモデルであり、その少し前に登場したSeq2Seqから派生したモデルです。
- Seq2Seq: https://arxiv.org/abs/1409.3215
予測・出力のイメージはSeq2Seqと同様、入力シーケンスと出力シーケンスがあり、TSPにおいては、入力は都市の位置関係情報として都市ポイントの列を与え、予測は巡回する都市ポイントの列を出力させます。
これにPtr-Netと呼ばれる機構を導入する工夫がなされており、入力ポイントを直接参照するAttentionに近い仕組みで都市を重複して回らないようにしています。
早速、PyTorchによる実装例は以下のようになります。
class Attention(nn.Module):
def __init__(self, hidden_size, use_tanh=False, C=10, use_cuda=use_cuda):
super(Attention, self).__init__()
self.use_tanh = use_tanh
self.C = C
# Bahdanau algo
self.W_query = nn.Linear(hidden_size, hidden_size)
self.W_ref = nn.Conv1d(hidden_size, hidden_size, 1, 1)
V = torch.cuda.FloatTensor(hidden_size) if use_cuda else torch.FloatTensor(hidden_size)
self.V = nn.Parameter(V)
self.V.data.uniform_(-(1. / math.sqrt(hidden_size)) , 1. / math.sqrt(hidden_size))
def forward(self, query, ref):
# query = [batch_size, hidden_size]
# ref = [batch_size, seq_len, hidden_size]
batch_size = ref.size(0)
seq_len = ref.size(1)
# Bahdanau algo
ref = ref.permute(0, 2, 1)
query = self.W_query(query).unsqueeze(2) # [batch_size x hidden_size x 1]
ref = self.W_ref(ref) # [batch_size x hidden_size x seq_len]
expanded_query = query.repeat(1, 1, seq_len) # [batch_size x hidden_size x seq_len]
V = self.V.unsqueeze(0).unsqueeze(0).repeat(batch_size, 1, 1) # [batch_size x 1 x hidden_size]
logits = torch.bmm(V, torch.tanh(expanded_query + ref)).squeeze(1)
if self.use_tanh:
logits = self.C * torch.tanh(logits)
return ref, logits
class GraphEmbedding(nn.Module):
def __init__(self, input_size, embedding_size, use_cuda=use_cuda):
super(GraphEmbedding, self).__init__()
self.embedding_size = embedding_size
self.use_cuda = use_cuda
self.embedding = nn.Parameter(torch.FloatTensor(input_size, embedding_size))
self.embedding.data.uniform_(-(1. / math.sqrt(embedding_size)), 1. / math.sqrt(embedding_size))
def forward(self, inputs):
# inputs = [batch_size, input_size, seq_len]
batch_size = inputs.size(0)
seq_len = inputs.size(2)
embedding = self.embedding.repeat(batch_size, 1, 1)
embedded = []
inputs = inputs.unsqueeze(1)
for i in range(seq_len):
embedded.append(torch.bmm(inputs[:, :, :, i].float(), embedding))
embedded = torch.cat(embedded, 1)
return embedded
class PointerNet(nn.Module):
def __init__(self, embedding_size, hidden_size, seq_len, n_glimpses, tanh_exploration, use_tanh, use_cuda=use_cuda):
super(PointerNet, self).__init__()
self.embedding_size = embedding_size
self.hidden_size = hidden_size
self.n_glimpses = n_glimpses
self.seq_len = seq_len
self.use_cuda = use_cuda
self.embedding = GraphEmbedding(2, embedding_size, use_cuda=use_cuda)
self.encoder = nn.LSTM(embedding_size, hidden_size, batch_first=True)
self.decoder = nn.LSTM(embedding_size, hidden_size, batch_first=True)
self.pointer = Attention(hidden_size, use_tanh=use_tanh, C=tanh_exploration, use_cuda=use_cuda)
self.glimpse = Attention(hidden_size, use_tanh=False, use_cuda=use_cuda)
self.decoder_start_input = nn.Parameter(torch.FloatTensor(embedding_size))
self.decoder_start_input.data.uniform_(-(1. / math.sqrt(embedding_size)), 1. / math.sqrt(embedding_size))
def apply_mask_to_logits(self, logits, mask, idxs):
batch_size = logits.size(0)
clone_mask = mask.clone()
if idxs is not None:
clone_mask[[i for i in range(batch_size)], idxs.data] = 1
logits[clone_mask] = -np.inf
return logits, clone_mask
def forward(self, inputs):
# inputs = [batch_size, 1, seq_len]
batch_size = inputs.size(0)
seq_len = inputs.size(2)
embedded = self.embedding(inputs)
encoder_outputs, (hidden, context) = self.encoder(embedded)
prev_probs = []
prev_idxs = []
mask = torch.zeros(batch_size, seq_len).byte().cuda() if self.use_cuda else torch.zeros(batch_size, seq_len).byte()
idxs = None
decoder_input = self.decoder_start_input.unsqueeze(0).repeat(batch_size, 1)
for i in range(seq_len):
_, (hidden, context) = self.decoder(decoder_input.unsqueeze(1), (hidden, context))
query = hidden.squeeze(0)
for i in range(self.n_glimpses):
ref, logits = self.glimpse(query, encoder_outputs)
logits, mask = self.apply_mask_to_logits(logits, mask, idxs)
query = torch.bmm(ref, F.softmax(logits).unsqueeze(2)).squeeze(2)
_, logits = self.pointer(query, encoder_outputs)
logits, mask = self.apply_mask_to_logits(logits, mask, idxs)
probs = F.softmax(logits)
idxs = probs.multinomial(num_samples=1).squeeze(1)
for old_idxs in prev_idxs:
if old_idxs.eq(idxs).data.any():
idxs = probs.multinomial(num_samples=1).squeeze(1)
break
decoder_input = embedded[[i for i in range(batch_size)], idxs.data, :]
prev_probs.append(probs)
prev_idxs.append(idxs)
return prev_probs, prev_idxs続いて、学習の方法についてですが、前述のPointer Networkの論文でもTSPへの適用は言及されており、そこでは最適化手法で得られた最適解を教師データとして学習させていました。
一方で、下記論文にて、深層強化学習の枠組みとして考えることで、探索的に最適巡回経路を求める学習方法が提案されています。
- Neural Combinatorial Optimization with Reinforcement Learning: https://arxiv.org/abs/1611.09940

ここで報酬は負の総移動距離とし、ポリシーで提案した移動経路の総移動距離が短くなるほど、報酬が上昇するという形にしています。
PyTorchによる実装例は以下のようになります。
def reward(sample_solution, use_cuda=use_cuda):
batch_size = sample_solution[0].size(0)
n = len(sample_solution) # sample_solution is seq_len of [batch_size]
tour_len = Variable(torch.zeros([batch_size])).cuda() if use_cuda else Variable(torch.zeros([batch_size]))
for i in range(n - 1):
tour_len += torch.norm(sample_solution[i] - sample_solution[i + 1], dim=1)
tour_len += torch.norm(sample_solution[n - 1] - sample_solution[0], dim=1)
return tour_len
class NeuralCombinatorialOptimization(nn.Module):
def __init__(self, embedding_size, hidden_size, seq_len, n_glimpses, tanh_exploration, use_tanh, reward, use_cuda=use_cuda):
super(NeuralCombinatorialOptimization, self).__init__()
self.reward = reward
self.use_cuda = use_cuda
self.actor = PointerNet(embedding_size, hidden_size, seq_len, n_glimpses, tanh_exploration, use_tanh, use_cuda)
def forward(self, inputs):
# inputs = [batch_size, input_size, seq_len]
batch_size = inputs.size(0)
input_size = inputs.size(1)
seq_len = inputs.size(2)
probs, action_idxs = self.actor(inputs)
actions = []
inputs = inputs.transpose(1, 2)
for action_id in action_idxs:
actions.append(inputs[[x for x in range(batch_size)], action_id.data, :])
action_probs = []
for prob, action_id in zip(probs, action_idxs):
action_probs.append(prob[[x for x in range(batch_size)], action_id.data])
R = self.reward(actions, self.use_cuda)
return R, action_probs, actions, action_idxsこれを、PuLPで解いてみた場合と比較してみます。
実際に再度適当にTSPを用意して、PuLPで解いてみました。
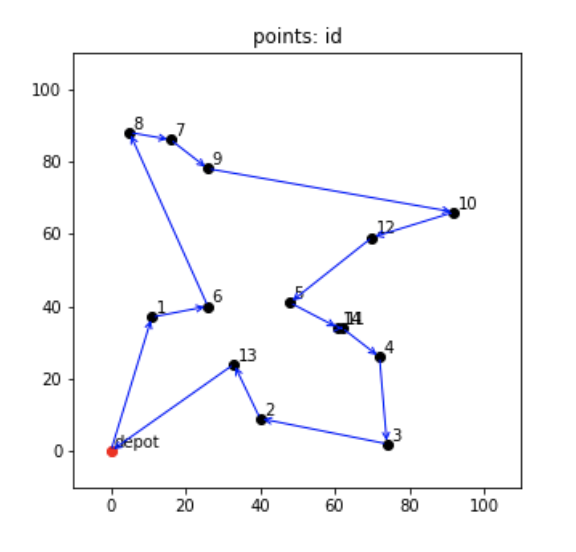
総移動距離は393となりました。
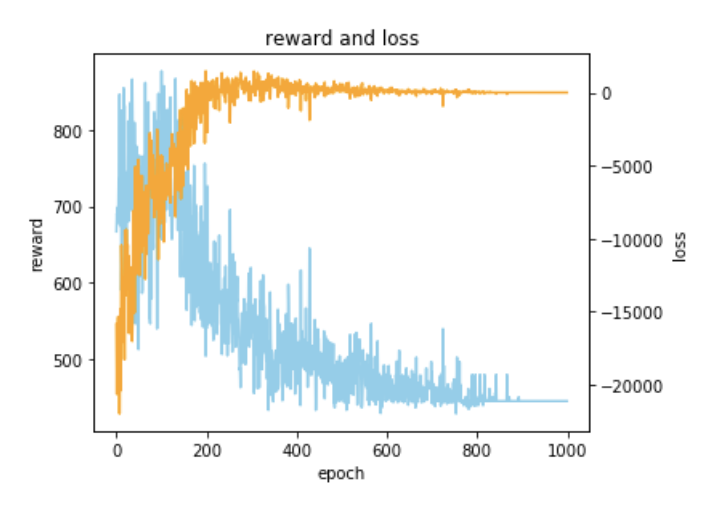
一方で、Pointer Networkを用いた深層強化学習で学習させてみた学習過程が以下になります。
最適解であった393に近い、445で学習を終えていそうな感じがわかります。

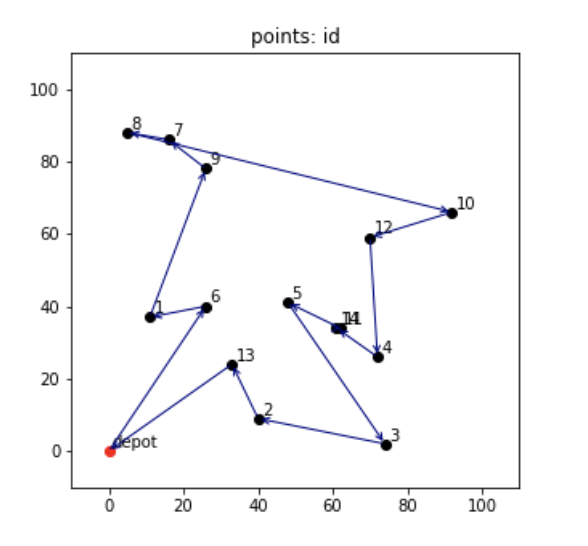
学習させたモデルで最短経路を予測させ、可視化させたものが以下のようになります。
最適解にちょっと惜しいようなルートが可視化されました。
まとめ
TSPやVRPにおいて、PuLPで最適解を求める例と、深層強化学習によるアプローチをご紹介しました。
最近数理最適化も勉強しているのですが、機械学習・深層学習とも異なるし、統計学・ベイズなどとも異なる感じで難しいですね。
ここでご紹介した実装例のように、シミュレーションやエージェントのようにプログラムで最適化したい対象を模写して動かしてみる感じではなく、定式化で行動の辻褄を合わせていくような感覚に近いので、直感的なイメージを頼りに作っていくようなものではない部分があります。
深層強化学習にアプローチについては、個人的にはもっと威力を発揮するかと思っていましたが、いまいち有効とは言い切れない感じな印象を受けました。
やはり問題自体の組み合わせ数に対して闇雲な探索はハードすぎるかもというところと、近年発展してきている深層学習・強化学習のテクニックをこちらの分野にまだあまり活用し切れていなさそうかと思いました。
正直なところ、位置情報を系列データで入力するメリット(順番で与える意味)は何か分かりませんでしたし…。
詳しく調べ切れてはいませんが、TransformerベースでVRPにアプローチする論文も提案されているみたいなので、まだまだ発展中の分野かもしれません。
また、こういった予測モデルで解くメリットとしては、大規模な問題かつ条件が頻繁に変わる(都市座標が毎回変わるなど)状態だと、有効な場合もあるかもと思いました。
最適化手法では毎回解くのに実行時間を要してしまいますが、深層強化学習のようなアプローチならランダムに都市情報を変えたデータでモデルを学習させておけば、毎回推論だけで済むと思います。
学習方法や探索方法をうまくドメイン的な要素も考慮し発展させていくことができれば、このような組み合わせ最適化問題に対する新しいアプローチも増えていきそうな気がしました。
